题目内容
17.已知一个口袋中装有n个红球(n≥1且n∈N)和2个白球,从中有放回地连续摸三次,每次摸出两个球,若两个球颜色不同则为中奖,否则不中奖.(1)当n=3时,设三次摸球中(每次摸球后放回)中奖的次数为ξ,求的ξ分布列;
(2)记三次摸球中(每次摸球后放回)恰有两次中奖的概率为P,当n取多少时,P最大.
分析 1)当n=3时,每次摸出两个球,中奖的概率p=$\frac{3×2}{{C}_{5}^{2}}$=$\frac{3}{5}$,设中奖次数为ζ,则ζ的可能取值为0,1,2,3.分别求出P(ζ=0),P(ζ=1),P(ζ=2),P(ζ=3),由此能求出ζ的分布列和Eζ.
(2)设每次摸奖中奖的概率为p,则三次摸球(每次摸球后放回)恰有两次中奖的概率为P(ζ=2)=${C}_{3}^{2}$•p2•(1-p)=-3p3+3p2,0<p<1,由此利用导数性质能求出n为1或2时,P有最大值.
解答 解(1)当n=3时,每次摸出两个球,中奖的概率$p=\frac{3×2}{C_5^2}=\frac{3}{5}$,
$P(ξ=0)=C_3^0{(\frac{2}{5})^3}=\frac{8}{125}$; $P(ξ=1)=C_3^1(\frac{3}{5}){(\frac{2}{5})^2}=\frac{36}{125}$;
$P(ξ=2)=C_3^2{(\frac{3}{5})^2}{(\frac{2}{5})^{\;}}=\frac{54}{125}$;$P(ξ=3)=C_3^3{(\frac{3}{5})^3}=\frac{27}{125}$;
ξ分布列为:
| ξ | 0 | 1 | 2 | 3 |
| p | $\frac{8}{125}$ | $\frac{36}{125}$ | $\frac{54}{125}$ | $\frac{27}{125}$ |
则三次摸球(每次摸奖后放回)恰有两次中奖的概率为:
$P(ξ=2)=C_3^2•{p^2}•(1-p)=-3{p^3}+6{p^2}$,0<p<1,
P'=-9p2+6p=-3p(3p-2),知在$(0,\frac{2}{3})$上P为增函数,在$(\frac{2}{3},1)$上P为减函数,
当$p=\frac{2}{3}$时P取得最大值.
又$p=\frac{4n}{(n+1)(n+2)}=\frac{2}{3}$,
故n2-3n+2=0,解得:n=1或n=2,
故n为1或2时,P有最大值.
点评 本题考查离散型随机变量的分布列和数学斯望的求法,解题时要认真审题,解题时要认真审题,注意导数的性质的灵活运用.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
8.已知点A(1,1),B(-2,2),则向量$\overrightarrow{OA}$与$\overrightarrow{BO}$的夹角为( ) (其中O为坐标原点)
| A. | 30° | B. | 90° | C. | 60° | D. | 120° |



 将边长分别为1、2、3、4、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形.由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为f(n).记数列{an}满足a1=1,an+1=$\left\{\begin{array}{l}f(n)\;\;当n为奇数\\ f({a_n})当n为偶数\end{array}$.
将边长分别为1、2、3、4、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形.由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为f(n).记数列{an}满足a1=1,an+1=$\left\{\begin{array}{l}f(n)\;\;当n为奇数\\ f({a_n})当n为偶数\end{array}$.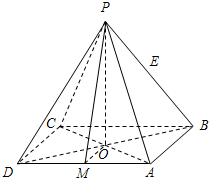 如图所示,四棱锥P-ABCD中,PA=PB=PC=PD,AB=a,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$.
如图所示,四棱锥P-ABCD中,PA=PB=PC=PD,AB=a,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$.