题目内容
4.已知函数f(x)=sin(x+φ)-2cos(x+φ)(0<φ<π)的图象关于直线x=π对称,则cos2φ=( )| A. | $\frac{3}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
分析 由题意可得f($\frac{π}{2}$)=f($\frac{3π}{2}$),化简可得tanφ的值,再根据cos2φ=$\frac{{cos}^{2}φ{-sin}^{2}φ}{{cos}^{2}φ{+sin}^{2}φ}$=$\frac{1{-tan}^{2}φ}{1{+tan}^{2}φ}$,计算求的结果.
解答 解:∵函数f(x)=sin(x+φ)-2cos(x+φ)(0<φ<π)的图象关于直线x=π对称,
∴f($\frac{π}{2}$)=f($\frac{3π}{2}$),即 cosφ+2sinφ=-cosφ-2sinφ,即cosφ=-2sinφ,即tanφ=-$\frac{1}{2}$,
则cos2φ=$\frac{{cos}^{2}φ{-sin}^{2}φ}{{cos}^{2}φ{+sin}^{2}φ}$=$\frac{1{-tan}^{2}φ}{1{+tan}^{2}φ}$=$\frac{1-\frac{1}{4}}{1+\frac{1}{4}}$=$\frac{3}{5}$,
故选:A.
点评 本题主要考查三角函数的图象的对称性,同角三角函数的基本关系、二倍角公式的应用,属于基础题.

练习册系列答案
相关题目
12.某公司在销售某种环保材料过程中,记录了每日的销售量x(吨)与利润y(万元)的对应数据,下表是其中的几组对应数据,由此表中的数据得到了y关于x的线性回归方程$\widehat{y}$=0.7x+a,若每日销售量达到10吨,则每日利润大约是( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | 7.2万元 | B. | 7.35万元 | C. | 7.45万元 | D. | 7.5万元 |
19.已知集合A={x|1<2x≤16},B={x|x<a},若A∩B=A,则实数a的取值范围是( )
| A. | a>4 | B. | a≥4 | C. | a≥0 | D. | a>0 |
8.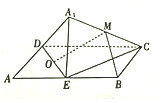 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )| A. | 与平面A1DE垂直的直线必与直线BM垂直 | |
| B. | 过E作EG∥BM,G∈平面A1DC,则∠A1EG为定值 | |
| C. | 一定存在某个位置,使DE⊥MO | |
| D. | 三棱锥A1-ADE外接球半径与棱AD的长之比为定值 |