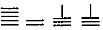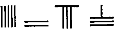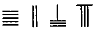题目内容
12.某公司在销售某种环保材料过程中,记录了每日的销售量x(吨)与利润y(万元)的对应数据,下表是其中的几组对应数据,由此表中的数据得到了y关于x的线性回归方程$\widehat{y}$=0.7x+a,若每日销售量达到10吨,则每日利润大约是( )| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | 7.2万元 | B. | 7.35万元 | C. | 7.45万元 | D. | 7.5万元 |
分析 求出样本中心坐标,代入回归直线方程,求解即可.
解答 解:由题意可知:$\overline{x}$=4.5,$\overline{y}$=3.5
因为回归直线经过样本中心,所以3.5=0.7×4.5+a,
解得a=0.35.
∴$\widehat{y}$=0.7x+0.35,
x=10吨时,$\widehat{y}$=7.35万元,
故选:B.
点评 本题考查回归直线方程的应用,回归直线经过样本中心是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20. 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=cos(ω+$\frac{π}{3}$)的图象,则只将f(x)的图象( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=cos(ω+$\frac{π}{3}$)的图象,则只将f(x)的图象( )
 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=cos(ω+$\frac{π}{3}$)的图象,则只将f(x)的图象( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=cos(ω+$\frac{π}{3}$)的图象,则只将f(x)的图象( )| A. | 向左平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{12}$个单位 |
4.已知函数f(x)=sin(x+φ)-2cos(x+φ)(0<φ<π)的图象关于直线x=π对称,则cos2φ=( )
| A. | $\frac{3}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
2.若不等式ln(x+2)+a(x2+x)≥0对于任意的x∈[-1,+∞)恒成立,则实数a的取值范围是( )
| A. | [0,+∞) | B. | [0,1] | C. | [0,e] | D. | [-1,0] |
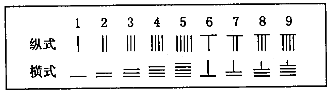
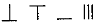 ,则5288用算筹式可表示为( )
,则5288用算筹式可表示为( )