题目内容
(
x-2y)5的展开式中的x2y3系数是 .
| 1 |
| 2 |
考点:二项式系数的性质
专题:二项式定理
分析:先求得二项展开式的通项公式,令x的幂指数等于2、y的幂指数等于3,可得r的值,即可求得x2y3系数.
解答:
解:(
x-2y)5的展开式的通项公式为Tr+1=
•(-2)r•(
)5-r•x5-r•yr,
令r=3,可得x2y3系数是-20,
故答案为:-20.
| 1 |
| 2 |
| C | r 5 |
| 1 |
| 2 |
令r=3,可得x2y3系数是-20,
故答案为:-20.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
要得到函数y=sin(2x-
)的图象,可由函数y=sinx( )
| π |
| 4 |
A、向右平移
| ||||
B、将图象上所有点横坐标变为原来的2倍,纵坐标不变,再向右平移
| ||||
C、向右平移
| ||||
D、将图象上所有点横坐标变为原来的
|
若a、b是任意实数,且a>b,则下列不等式恒成立的是( )
| A、a2>b2 | ||||
B、
| ||||
| C、lg(a-b)>0 | ||||
D、(
|
已知点A(a,6)到直线3x-4y=2的距离为4,则a=( )
| A、2 | ||
B、
| ||
C、2或
| ||
D、14或
|
已知向量
=(m,1),
=(m2,2),若存在A∈R,使得
+λ
=
,则m=( )
| a |
| b |
| a |
| b |
| 0 |
| A、0 | B、2 | C、0或2 | D、0或-2 |
函数y=cosx,x∈R的最小正周期是( )
| A、4π | ||
| B、2π | ||
| C、π | ||
D、
|
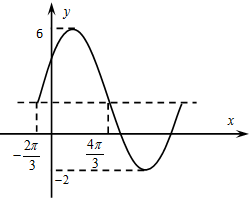 已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,|φ|<