题目内容
函数y=cosx，x∈R的最小正周期是（ ）
| A、4π | ||
| B、2π | ||
| C、π | ||
D、
|
考点：三角函数的周期性及其求法
专题：三角函数的求值
分析：直接利用三角函数的周期公式求解即可．
解答：
解：函数y=cosx，x∈R的最小正周期是：
=2π．
故选：B．
| 2π |
| 1 |
故选：B．
点评：本题考查余弦函数周期的求法，考查计算能力．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知p，q∈R，则“q＜p＜0”是“|
|＜1”的（ ）
| p |
| q |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
已知-
≤α＜β≤
，则
的范围是（ ）
| π |
| 2 |
| π |
| 2 |
| α-β |
| 2 |
A、（-
| ||
B、[-
| ||
C、（-
| ||
D、[-
|
等差数列1，4，7…的第4项是（ ）
| A、8 | B、9 | C、10 | D、11 |
等比数列{an}的前n项和为Sn，且S3=14，a1=2，则a4=（ ）
| A、16 | B、16或-16 |
| C、-54 | D、16或-54 |
函数f（x）=
的定义域是（ ）
| x-1 |
| A、{x|x＜1} |
| B、{x|x≤1} |
| C、{x|x＞1} |
| D、{x|x≥1} |
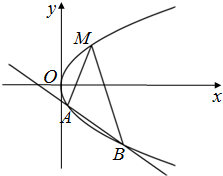如图所示，已知点M（a，3）是抛物线y2=4x上一定点，直线AM、BM的斜率互为相反数，且与抛物线另交于A、B两个不同的点．