题目内容
过双曲线
-
=1的右焦点F2作实轴的垂线，交双曲线于A、B两点．
（1）求线段AB的长；
（2）若△AF1F2为等腰直角三角形，求双曲线的离心率（F1为左焦点）．
| x2 |
| a2 |
| y2 |
| b2 |
（1）求线段AB的长；
（2）若△AF1F2为等腰直角三角形，求双曲线的离心率（F1为左焦点）．
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：（1）直接把右焦点坐标代入双曲线方程求得A，B的纵坐标，则答案可求；
（2）由△AF1F2为等腰直角三角形可得
=2c，借助于隐含条件转化为关于e的方程得答案．
（2）由△AF1F2为等腰直角三角形可得
| b2 |
| a |
解答：
解：（1）作出双曲线
-
=1的图象如图，
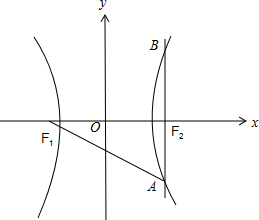
∵F2（c，0），在双曲线方程中，取x=c，得y2=
，
∴y=±
．
∴|AB|=
；
（2）若△AF1F2为等腰直角三角形，
则
=2c，即c2-a2=2ac，
e2-2e-1=0，解得e=
+1．
| x2 |
| a2 |
| y2 |
| b2 |
∵F2（c，0），在双曲线方程中，取x=c，得y2=
| b4 |
| a2 |
∴y=±
| b2 |
| a |
∴|AB|=
| 2b2 |
| a |
（2）若△AF1F2为等腰直角三角形，
则
| b2 |
| a |
e2-2e-1=0，解得e=
| 2 |
点评：本题考查了双曲线的简单几何性质，考查了数形结合的解题思想方法，是基础的计算题．
练习册系列答案
相关题目
已知a=0.3-2，b=(
)0.3，c=(
)0.2，则a，b，c的大小关系是（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、a＞b＞c |
| B、a＞c＞b |
| C、c＞b＞a |
| D、b＞a＞c |
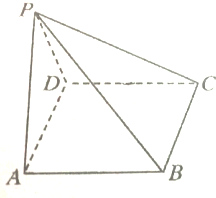如图所示，在四棱锥P-ABCD中，底面ABCD是矩形，且PA⊥平面ABCD，PA=5，AB=4，AD=3，求直线PC与平面ABCD所成的角．