在${^6}$的展开式中常数项的系数是60.则a的值为2．题目和参考答案——青夏教育精英家教网—

题目内容

8．在${（\sqrt{x}+\frac{a}{x}）^6}（a＞0）$的展开式中常数项的系数是60，则a的值为2．

分析利用通项公式即可得出．

解答解：T_r+1=${∁}_{6}^{r}$$（\sqrt{x}）^{6-r}（\frac{a}{x}）^{r}$=a^r${∁}_{6}^{r}{x}^{3-\frac{3r}{2}}$，
令3-$\frac{3r}{2}$=0，解得r=2．
∴${a}^{2}{∁}_{6}^{2}$=60，a＞0，解得a=2．
故答案为：2．

点评本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题．

练习册系列答案

19．已知定义在R上的偶函数f（x）在[0，+∞）上递减，且f（1）=0，则不等式f（log₄x）+f（log$\frac{1}{4}$x）≥0的解集为[$\frac{1}{4}$，4]．

16．设集合M={x|x=2k+1，k∈Z}，N={x|x=k+2，k∈Z}，则．（　　）

3．已知$\overline z$是z的共轭复数，若$\overline z+z=2，（\overline z-z）i=2$（其中i为虚数单位），则z的值为（　　）

13．在直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}x=1+tcosα\\ y=2+tsinα\end{array}\right.（t$为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴非负半轴为极轴）中，圆C的方程为ρ=6sinθ
（1）求圆C的直角坐标方程；
（2）若点P（1，2），设圆C与直线l交于点A、B，求$\frac{1}{{|{PA}|}}+\frac{1}{{|{PB}|}}$的最小值．

20．设p：x＜2，q：-2＜x＜2，则p是q成立的（　　）

	A．	充分非必要条件		B．	必要非充分条件
	C．	充要条件		D．	既不充分也不必要条件

17．

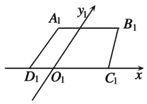如图，梯形A₁B₁C₁D₁是一平面图形ABCD的直观图（斜二测），若AD∥Oy，AB∥CD，A₁B₁=$\frac{3}{4}{C_1}{D_1}=3，{A_1}{D_1}$=1，则原平面图形ABCD的面积是（　　）

10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点M（2，1），且离心率为$\frac{\sqrt{3}}{2}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若过原点的直线l₁与椭圆C交于P，Q两点，且在直线l₂：x-y+2$\sqrt{6}$=0上存在点M，使得△MPQ为等边三角形，求直线l₁的方程．

试题分类