题目内容
15.已知$sin(α+\frac{π}{6})=\frac{1}{3}$,则$cos(2α-\frac{2π}{3})$的值是( )| A. | $\frac{5}{9}$ | B. | $-\frac{8}{9}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{7}{9}$ |
分析 由$sin(α+\frac{π}{6})=\frac{1}{3}$求出cos(2α+$\frac{π}{3}$)的值,再根据诱导公式即可求出$cos(2α-\frac{2π}{3})$的值.
解答 解:∵$sin(α+\frac{π}{6})=\frac{1}{3}$,
∴cos(2α+$\frac{π}{3}$)=cos[2(α+$\frac{π}{6}$)]
=1-2sin2(α+$\frac{π}{6}$)
=1-2×${(\frac{1}{3})}^{2}$
=$\frac{7}{9}$;
∴$cos(2α-\frac{2π}{3})$=cos[2α+($\frac{π}{3}$-π)]
=cos[π-(2α+$\frac{π}{3}$)]
=-cos(2α+$\frac{π}{3}$)
=-$\frac{7}{9}$.
故选:D.
点评 本题考查了三角恒等变换与诱导公式的应用问题,是基础题目.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
5.设函数y=f(x),x∈R“y=|f(x)|是偶函数”是“y=f(x)的图象关于原点对称”的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
6.在正方体ABCD-A1B1C1D1中,直线AB1与平面ABC1D1所成的角的正弦值为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
3.已知$\overline z$是z的共轭复数,若$\overline z+z=2,(\overline z-z)i=2$(其中i为虚数单位),则z的值为( )
| A. | 1-i | B. | -1-i | C. | -1+i | D. | 1+i |
20.设p:x<2,q:-2<x<2,则p是q成立的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
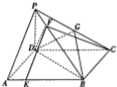 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.