题目内容
5．某四棱锥的三视图如图所示，该四棱锥的表面积是（ ）
| A． | 32 | B． | 16+16$\sqrt{2}$ | C． | 48 | D． | 16+32$\sqrt{2}$ |
分析 由已知中的三视图，可得四棱锥的底面棱长为4，高为2，求出侧高后，代入棱锥表面积公式，可得答案．
解答 解：由已知中的三视图，可得四棱锥的底面棱长为4，
故底面面积为：16，
棱锥的高为2，
故棱锥的侧高为：$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$，
故棱锥的侧面积为：4×$\frac{1}{2}$×4×$2\sqrt{2}$=16$\sqrt{2}$，
故棱锥的表面积为：16+16$\sqrt{2}$，
故选：B
点评 本题考查的知识点是棱柱的体积和表面积，棱锥的体积和表面积，简单几何体的三视图，难度基础．
练习册系列答案
名校课堂系列答案
相关题目
15．已知x，y满足线性约束条件$\left\{\begin{array}{l}y-x≤3\\ x+y≤5\\ y≥λ\end{array}\right.$，若z=x+4y的最大值与最小值之差为5，则实数λ的值为（ ）
| A． | 3 | B． | $\frac{7}{3}$ | C． | $\frac{3}{2}$ | D． | 1 |
16．设集合M={x|x=2k+1，k∈Z}，N={x|x=k+2，k∈Z}，则．（ ）
| A． | M=N | B． | M?N | C． | N?M | D． | M∩N=∅ |
20．设p：x＜2，q：-2＜x＜2，则p是q成立的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
10．已知函数$f（x）=\frac{3x}{a}-2{x^2}+lnx$，其中a为常数．
（1）若a=1，求函数f（x）的单调区间；
（2）若函数f（x）在区间[1，2]上为单调增函数，求a的取值范围．
（1）若a=1，求函数f（x）的单调区间；
（2）若函数f（x）在区间[1，2]上为单调增函数，求a的取值范围．
17．
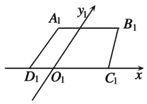如图，梯形A1B1C1D1是一平面图形ABCD的直观图（斜二测），若AD∥Oy，AB∥CD，A1B1=$\frac{3}{4}{C_1}{D_1}=3，{A_1}{D_1}$=1，则原平面图形ABCD的面积是（ ）
如图，梯形A1B1C1D1是一平面图形ABCD的直观图（斜二测），若AD∥Oy，AB∥CD，A1B1=$\frac{3}{4}{C_1}{D_1}=3，{A_1}{D_1}$=1，则原平面图形ABCD的面积是（ ）| A． | 14． | B． | 7 | C． | $14\sqrt{2}$ | D． | $7\sqrt{2}$ |