题目内容
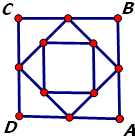正方形ABCD的边长为1，选各边的中点按如图连成正方形，再选各边中点连成正方形，依次无限做下去，则所有正方形的边长之和为（ ）| A、5 | ||
| B、6 | ||
C、2+
| ||
| D、8 |
考点：数列的应用,等比数列的前n项和
专题：应用题,规律型
分析：由题意，所有正方形的边长组成以1为首项，
为公比的等比数列，利用等比数列的求和公式，即可得出结论．
| ||
| 2 |
解答：
解：由题意，所有正方形的边长组成以1为首项，
为公比的等比数列，
∴所有正方形的边长和为S=
=2+
．
故选：C．
| ||
| 2 |
∴所有正方形的边长和为S=
| 1 | ||||
1-
|
| 2 |
故选：C．
点评：解题的关键是掌握中位线定理和正方形的性质，确定所有正方形的边长组成以1为首项，
为公比的等比数列．
| ||
| 2 |
练习册系列答案
智慧小复习系列答案
相关题目
已知F为抛物线x2=2py（p＞0）的焦点，M为其上一点，且|MF|=2p，则直线MF的斜率为（ ）
A、-
| ||||
B、±
| ||||
C、-
| ||||
D、±
|
曲线y=x3-2x+4在点（-1，5）处的切线的倾斜角为（ ）
| A、45° | B、60° |
| C、120° | D、135° |
下列三角函数值：
①sin（nπ+
π）（n∈Z）；
②sin（2nπ+
）（n∈Z）；
③sin[（2n+1）π-
]（n∈Z），
其中，函数值与sin
的值相同的是（ ）
①sin（nπ+
| 4 |
| 3 |
②sin（2nπ+
| π |
| 3 |
③sin[（2n+1）π-
| π |
| 3 |
其中，函数值与sin
| π |
| 3 |
| A、①② | B、③ | C、②③ | D、② |
若直线l不平行于平面 α，且l?α，则（ ）
| A、α内不存在与l平行的直线 |
| B、α内的所有直线与l异面 |
| C、α内存在唯一的直线与l平行 |
| D、α内的直线与l都相交 |