题目内容
正三棱柱ABC-A1B1C1中,AB=2,AA1=1,D为A1C1的中点,线段B1C上的点M满足向量
=λ
,若
与
的夹角小于45°,求实数λ的值.
| B1M |
| B1C |
| AD |
| BM |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,建立空间直角坐标系.A(0,-1,1),D(
,-
,0),B(0,1,1),B1(0,1,0),C(
,0,1).利用向量的坐标运算可得点M的坐标,再利用向量的夹角公式即可得出.
| ||
| 2 |
| 1 |
| 2 |
| 3 |
解答:
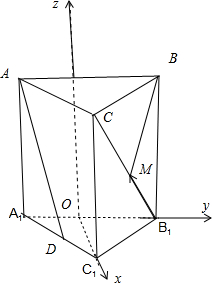 解:如图所示,建立空间直角坐标系.
解:如图所示,建立空间直角坐标系.
A(0,-1,1),D(
,-
,0),B(0,1,1),B1(0,1,0),C(
,0,1).
∵
=λ
,(λ∈[0,1]).
∴
=
+λ(
-
)=(1-λ)
+λ
=(1-λ)(0,1,0)+λ(
,0,1)=(
λ,1-λ,λ).
=(
,
,-1),
=(
λ,-λ,λ-1).
∴
•
=
λ-
λ+1-λ=1,|
|=
,|
|=
∵
与
的夹角小于45°,
∴
≥cos45°,
∴
≥
,
化为5λ2-2λ≤0,解得0≤λ≤
.
∴λ的取值范围是[0,
].
 解:如图所示,建立空间直角坐标系.
解:如图所示,建立空间直角坐标系.A(0,-1,1),D(
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∵
| B1M |
| B1C |
∴
| OM |
| OB1 |
| OC |
| OB1 |
| OB1 |
| OC |
| 3 |
| 3 |
| AD |
| ||
| 2 |
| 1 |
| 2 |
| BM |
| 3 |
∴
| AD |
| BM |
| 3 |
| 2 |
| 1 |
| 2 |
| AD |
| 2 |
| BM |
| 5λ2-2λ+1 |
∵
| AD |
| BM |
∴
| ||||
|
|
∴
| 1 | ||||
|
| ||
| 2 |
化为5λ2-2λ≤0,解得0≤λ≤
| 2 |
| 5 |
∴λ的取值范围是[0,
| 2 |
| 5 |
点评:本题考查了向量的坐标运算、向量的夹角公式、余弦函数的单调性,考查了计算能力,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
已知函数f(x),当自变量x由x0增加到x0+△x时,函数值的增量与自变量的增量的比值为( )
| A、函数在x0处的变化率 |
| B、函数在区间[x0,x0+△x]上的平均变化率 |
| C、函数在x0+△x处的变化率 |
| D、函数在x0处的导数 |
平行于同一条直线的两条直线间的位置关系是( )
| A、异面 | B、平行 |
| C、相交 | D、以上都有可能 |
若a>0,b>0且4a2+b2=4,则a
的最大值是( )
| 1+b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
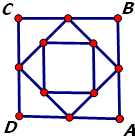 正方形ABCD的边长为1,选各边的中点按如图连成正方形,再选各边中点连成正方形,依次无限做下去,则所有正方形的边长之和为( )
正方形ABCD的边长为1,选各边的中点按如图连成正方形,再选各边中点连成正方形,依次无限做下去,则所有正方形的边长之和为( )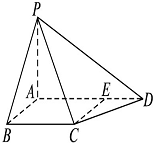 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.