题目内容
曲线y=x3-2x+4在点（-1，5）处的切线的倾斜角为（ ）
| A、45° | B、60° |
| C、120° | D、135° |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：先求该点处的导数，即切线斜率，由斜率定义即可求得倾斜角．
解答：
解：∵y=x3-2x+4，
∴y′=3x2-2，
x=-1时，切线的斜率k=3×（-1）2-2=1．
故倾斜角为45°．
故选：A．
∴y′=3x2-2，
x=-1时，切线的斜率k=3×（-1）2-2=1．
故倾斜角为45°．
故选：A．
点评：本题考查利用导数研究曲线上某点切线方程，属中档题，正确理解导数的几何意义是解决题目的基础，注意倾斜角的范围．
练习册系列答案
相关题目
若函数f（x）=Asin（ωx+φ）+1（ω＞0，|φ|＜π）对任意实数t，都有f（t+
）=f（-t+
），记g（x）=Acos（ωx+φ）-1，则g（
）=（ ）
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
已知函数f（x），当自变量x由x0增加到x0+△x时，函数值的增量与自变量的增量的比值为（ ）
| A、函数在x0处的变化率 |
| B、函数在区间[x0，x0+△x]上的平均变化率 |
| C、函数在x0+△x处的变化率 |
| D、函数在x0处的导数 |
已知函数f（x）定义域是R，满足对任意的x1＜x2，都有
＞0，且A（0，-2），B（3，2）是其图象上的两点，那么|f（x+1）|＜2的解集是（ ）
| f(x1)-f(x2) |
| x1-x2 |
| A、（1，4） |
| B、（-1，2） |
| C、（-∞，1）∪[4，+∞] |
| D、（-∞，-1）∪[2，+∞） |
下列函数中，最小值为6的是（ ）
A、y=x+
| ||
| B、y=ex+9•e-x | ||
C、y=sinx+
| ||
| D、y=log2x+9logx2 |
如图所示的程序框图，运行相应的程序，若输入x的值为4，则输出y的值为（ ）
| A、2 | B、4 | C、8 | D、16 |
平行于同一条直线的两条直线间的位置关系是（ ）
| A、异面 | B、平行 |
| C、相交 | D、以上都有可能 |
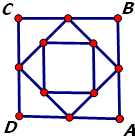正方形ABCD的边长为1，选各边的中点按如图连成正方形，再选各边中点连成正方形，依次无限做下去，则所有正方形的边长之和为（ ）
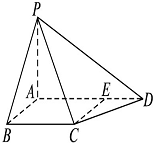如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB．