题目内容
已知F为抛物线x2=2py（p＞0）的焦点，M为其上一点，且|MF|=2p，则直线MF的斜率为（ ）
A、-
| ||||
B、±
| ||||
C、-
| ||||
D、±
|
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：先确定M的坐标，再计算直线MF的斜率．
解答：
解：根据定义，点M与准线的距离也是2p，
设M（x0，y0），则M与准线的距离为：y0+
=2p，
∴y0=
p，
∴x0=±
p，
∵F（0，
），
∴直线MF的斜率为
=±
．
故选：B．
设M（x0，y0），则M与准线的距离为：y0+
| p |
| 2 |
∴y0=
| 3 |
| 2 |
∴x0=±
| 3 |
∵F（0，
| p |
| 2 |
∴直线MF的斜率为
| ||||
±
|
| ||
| 3 |
故选：B．
点评：本题考查了抛物线的定义和性质，解题的关键是根据定义得出点M与焦点F的距离等于M到准线的距离，属于基础题．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
若函数f（x）=Asin（ωx+φ）+1（ω＞0，|φ|＜π）对任意实数t，都有f（t+
）=f（-t+
），记g（x）=Acos（ωx+φ）-1，则g（
）=（ ）
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
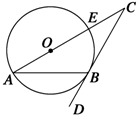如图所示，CD切⊙O于B，CO的延长线交⊙O于A，若∠C=36°，则∠ABD的度数是（ ）| A、72° | B、63° |
| C、54° | D、36° |
已知在△ABC中，BC=6，AB=4，cosB=
，则AC=（ ）
| 1 |
| 3 |
| A、6 | ||
B、2
| ||
C、3
| ||
D、4
|
下列关于函数f（x）=sin（2x+
）的结论：
①f（x）的最小正周期是2π；
②f（x）在区间[kπ-
，kπ+
]（k∈Z）上单调递增；
③当x∈[0，
]时，f（x）的值域为[-
，
]；
④函数y=f（x+
）是偶函数．
其中正确的结论为（ ）
| π |
| 3 |
①f（x）的最小正周期是2π；
②f（x）在区间[kπ-
| 5π |
| 12 |
| π |
| 12 |
③当x∈[0，
| π |
| 2 |
| ||
| 2 |
| ||
| 2 |
④函数y=f（x+
| π |
| 12 |
其中正确的结论为（ ）
| A、①② | B、②③ | C、②④ | D、③④ |
已知函数f（x），当自变量x由x0增加到x0+△x时，函数值的增量与自变量的增量的比值为（ ）
| A、函数在x0处的变化率 |
| B、函数在区间[x0，x0+△x]上的平均变化率 |
| C、函数在x0+△x处的变化率 |
| D、函数在x0处的导数 |
已知函数f（x）定义域是R，满足对任意的x1＜x2，都有
＞0，且A（0，-2），B（3，2）是其图象上的两点，那么|f（x+1）|＜2的解集是（ ）
| f(x1)-f(x2) |
| x1-x2 |
| A、（1，4） |
| B、（-1，2） |
| C、（-∞，1）∪[4，+∞] |
| D、（-∞，-1）∪[2，+∞） |
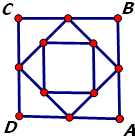正方形ABCD的边长为1，选各边的中点按如图连成正方形，再选各边中点连成正方形，依次无限做下去，则所有正方形的边长之和为（ ）