题目内容
把半圆弧分成4等份,以这些分点(包括直径的两端点)为顶点,作出三角形,从这些三角形中任取3个不同的三角形,则这3个不同的三角形中钝角三角形的个数X的期望为( )
A、
| ||
| B、2 | ||
| C、3 | ||
D、
|
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:一共能做出10个三角形,其中钝角三角形有7个,由题意知X=0,1,2,3,分别求出相应的概率,由此能求出钝角三角形的个数X的期望.
解答:
解:以这些分点(包括直径的两端点)为顶点,
一共能做出
=10个三角形,
其中钝角三角形有7个,
∴X=0,1,2,3,
P(X=0)=
=
,
P(X=1)=
=
,
P(X=2)=
=
,
P(X=3)=
=
,
∴EX=0×
+1×
+2×
+3×
=
.
故选:D.
一共能做出
| C | 2 5 |
其中钝角三角形有7个,
∴X=0,1,2,3,
P(X=0)=
| ||
|
| 1 |
| 120 |
P(X=1)=
| ||||
|
| 21 |
| 120 |
P(X=2)=
| ||||
|
| 63 |
| 120 |
P(X=3)=
| ||
|
| 35 |
| 120 |
∴EX=0×
| 1 |
| 120 |
| 21 |
| 120 |
| 63 |
| 120 |
| 35 |
| 120 |
| 21 |
| 10 |
故选:D.
点评:本题考查离散型随机变量的数学期望的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
相关题目
已知在△ABC中,BC=6,AB=4,cosB=
,则AC=( )
| 1 |
| 3 |
| A、6 | ||
B、2
| ||
C、3
| ||
D、4
|
下列函数中,最小值为6的是( )
A、y=x+
| ||
| B、y=ex+9•e-x | ||
C、y=sinx+
| ||
| D、y=log2x+9logx2 |
平行于同一条直线的两条直线间的位置关系是( )
| A、异面 | B、平行 |
| C、相交 | D、以上都有可能 |
已知回归直线方程的斜率的估计值是1.2,样本的中心点为(2,3),则回归直线方程是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若a>0,b>0且4a2+b2=4,则a
的最大值是( )
| 1+b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

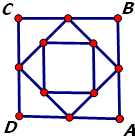 正方形ABCD的边长为1,选各边的中点按如图连成正方形,再选各边中点连成正方形,依次无限做下去,则所有正方形的边长之和为( )
正方形ABCD的边长为1,选各边的中点按如图连成正方形,再选各边中点连成正方形,依次无限做下去,则所有正方形的边长之和为( )