题目内容
4. 已知实数x,y的取值如表所示.
已知实数x,y的取值如表所示.| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 2 | 4 | 6 | 5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
注:回归方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,其中$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}$,a=$\overline y-b\overline x$.
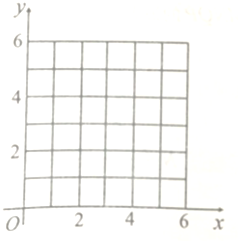
分析 (1)利用描点的方法绘制散点图;
(2)根据所给的这组数据求出利用最小二乘法所需要的几个数据,代入求系数b的公式,求得结果,再把样本中心点代入,求出a的值,得到线性回归方程.
解答 解:(1)散点图如下:
(2)$\overline x=\frac{0+1+2+3+4}{5}=2$,
$\overline y=\frac{1+2+4+6+5}{5}=3.6$,
$\sum_{i=1}^5{{x_i}{y_i}}=2+8+18+20=48$,
$\sum_{i=1}^4{x_i^2}=1+4+9+16=30$,
故$\widehat{b}$=$\frac{48-5×2×3.6}{30-5×4}$=1.2,则$\widehat{a}$=3.6-1.2×2=1.2,
所以回归直线的方程为$\hat{y}$=1.2x+1.2.
点评 本题考查线性回归方程,两个变量之间的关系,除了函数关系,还存在相关关系,通过建立回归直线方程,就可以根据其部分观测值,获得对这两个变量之间整体关系的了解.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
14.函数f(x)=$\frac{{\root{3}{x^2}}}{e^x}$在x∈[-2,2]上的极值点的位置有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
15.某公司在一次对员工的休闲方式(看电视与运动)与性别之间是否有关系的调查中,共调查了124人,其中女性70人中主要休闲方式是看电视的有43人,男性中主要休闲方式是运动的有33人.
(1)根据以上数据建立一个2×2的列联表;
(2)检验性别与休闲方式是否有关系.
${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
(1)根据以上数据建立一个2×2的列联表;
(2)检验性别与休闲方式是否有关系.
${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
| P(Χ2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
13.已知cosα=$\frac{1}{3}$,则cos2α=( )
| A. | $-\frac{5}{9}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | 1 | D. | $-\frac{7}{9}$ |
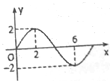 函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2017)=$\sqrt{2}$.
函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2017)=$\sqrt{2}$.