题目内容
2.己知x0=$\frac{π}{3}$是函数f(x)=sin(2x+φ)的一个极大值点,则f(x)的一个单调递减区间是( )| A. | ($\frac{π}{6}$,$\frac{2π}{3}$) | B. | ($\frac{π}{3}$,$\frac{5π}{6}$) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{2π}{3}$,π) |
分析 由极值点可得φ=-$\frac{π}{6}$,解2kπ+$\frac{π}{2}$<2x-$\frac{π}{6}$<2kπ+$\frac{3π}{2}$可得函数f(x)的单调递减区间,结合选项可得.
解答 解:∵x0=$\frac{π}{3}$是函数f(x)=sin(2x+φ)的一个极大值点,
∴sin(2×$\frac{π}{3}$+φ)=1,∴2×$\frac{π}{3}$+φ=2kπ+$\frac{π}{2}$,解得φ=2kπ-$\frac{π}{6}$,k∈Z,
不妨取φ=-$\frac{π}{6}$,此时f(x)=sin(2x-$\frac{π}{6}$)
令2kπ+$\frac{π}{2}$<2x-$\frac{π}{6}$<2kπ+$\frac{3π}{2}$可得kπ+$\frac{π}{3}$<x<kπ+$\frac{5π}{6}$,
∴函数f(x)的单调递减区间为(kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$)k∈Z,
结合选项可知当k=0时,函数的一个单调递减区间为($\frac{π}{3}$,$\frac{5π}{6}$),
故选:B.
点评 本题考查正弦函数的图象和单调性,数形结合是解决问题的关键,属基础题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
18.已知sinα=-$\frac{4}{5}$,α∈(π,$\frac{3π}{2}$),则tan$\frac{α}{2}$等于( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$或2 | D. | -2或$\frac{1}{2}$ |
11.为了得到函数g(x)=cos2x的图象,可以将f(x)=sin(2x+$\frac{π}{3}$)的图象( )
| A. | 向左平移$\frac{π}{12}$个单位长度 | B. | 向左平移$\frac{7π}{12}$个单位长度 | ||
| C. | 向右平移$\frac{π}{12}$个单位长度 | D. | 向右平移$\frac{7π}{12}$个单位长度 |
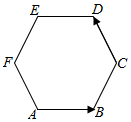
 如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=$∠IOA=\frac{π}{3}$,设$\overrightarrow{OD}=\vec a,\overrightarrow{OH}=\vec b$,已知点P在各菱形边上运动,且$\overrightarrow{OP}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,x,y∈R,则x+y的最大值为4.
如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=$∠IOA=\frac{π}{3}$,设$\overrightarrow{OD}=\vec a,\overrightarrow{OH}=\vec b$,已知点P在各菱形边上运动,且$\overrightarrow{OP}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,x,y∈R,则x+y的最大值为4.