题目内容
9.将函数y=sin2x的图象向左平移φ(φ>0)个单位,得到的图象恰好关于直线x=$\frac{π}{6}$对称,则φ的最小值是( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
分析 根据左加右减,写出三角函数平移后的解析式,根据平移后图象的对称轴,把对称轴代入使得函数式的值等于±1,写出自变量的值,根据求最小值得到结果.
解答 解:∵把函数y=sin2x的图象向右平移φ(φ>0)个单位,
∴平移后函数的解析式是y=sin(2x+2φ),
∵所得图象关于直线 x=$\frac{π}{6}$对称,
∴由正弦函数的图象和性质可得:2×$\frac{π}{6}$+2φ=kπ+$\frac{π}{2}$(k∈Z),解得:φ=$\frac{1}{2}$kπ+$\frac{π}{12}$(k∈Z),
∵φ>0
∴当k=0时,φ的最小值是$\frac{π}{12}$.
故选:A.
点评 本题考查由三角函数图象的平移求函数的解析式,本题解题的关键是先表示出函数的解析式,再根据题意来写出结果,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.已知i为虚数单位,复数z满足$\overline z(1+i)=i$,则z=( )
| A. | 1+i | B. | 1-i | C. | $\frac{1}{2}+\frac{1}{2}i$ | D. | $\frac{1}{2}-\frac{1}{2}i$ |
20.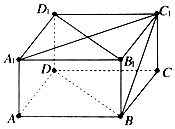 如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )
如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )
 如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )
如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{10}}{10}$ |
17.若sin(θ+3π)=$\frac{4}{5}$,tan(θ-π)>0,则cosθ=( )
| A. | $\frac{3}{5}$ | B. | $-\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{4}{5}$ |
4.下列函数中,既是奇函数又是增函数的是( )
| A. | y=x|x| | B. | y=-x3 | C. | y=$\frac{1}{x}$ | D. | y=sinx |
14.函数$f(x)=\frac{1}{x}$的导数是( )
| A. | $\frac{1}{x^2}$ | B. | $-\frac{1}{x^2}$ | C. | $\frac{1}{2x}$ | D. | $-\frac{1}{2x}$ |
13.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x,x>0}\\{(\frac{1}{3})^{x}-2,x≤0}\end{array}\right.$,则不等式f(x)≥1的解集为( )
| A. | {x|x≤-1} | B. | {x|x≥3} | C. | {x|x≤-1或x≥3} | D. | {x|x≤0或x≥3} |
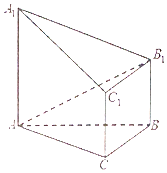 如图,已知AA1⊥平面ABC,BB1∥CC1∥AA1,$AC=\sqrt{3}$,$BC=\sqrt{2}$,AA1=2BB1=2CC1=2,BC⊥AC.
如图,已知AA1⊥平面ABC,BB1∥CC1∥AA1,$AC=\sqrt{3}$,$BC=\sqrt{2}$,AA1=2BB1=2CC1=2,BC⊥AC.