题目内容
10.在平面直角坐标系xOy中,圆C的参数方程为$\left\{\begin{array}{l}{x=4cosθ}\\{y=4sinθ}\end{array}\right.$(θ为参数),倾斜角a=$\frac{π}{6}$的直线l经过点P(1,2).(1)写出圆C的标准方程和直线l的参数方程;
(2)设直线l与圆C相交于A、B两点,求|PA|•|PB|的值.
分析 (1)根据sin2θ+cos2θ=1,消去θ得到圆的标准方程,根据倾斜角与直线l过点P,确定出直线l的参数方程即可;
(2)把直线方程代入圆方程,整理后利用韦达定理即可确定出所求式子的值.
解答 解:(1)$\left\{\begin{array}{l}{x=4cosθ}\\{y=4sinθ}\end{array}\right.$,
根据sin2θ+cos2θ=1,消去θ,得$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{16}$=1,
整理得:圆的标准方程为x2+y2=16,
∵倾斜角a=$\frac{π}{6}$的直线l经过点P(1,2),
∴直线l的参数方程为$\left\{\begin{array}{l}{x=1+t•cos\frac{π}{6}}\\{y=2+t•sin\frac{π}{6}}\end{array}\right.$,即$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=2+\frac{1}{2}t}\end{array}\right.$(t为参数);
(2)把直线l的方程$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=2+\frac{1}{2}t}\end{array}\right.$代入x2+y2=16中,得:(1+$\frac{\sqrt{3}}{2}$t)2+(2+$\frac{1}{2}$t)2=16,
整理得:t2+(2+$\sqrt{3}$)t-11=0,
由韦达定理得:t1t2=-11,
则|PA|•|PB|=11.
点评 此题考查了参数方程化为普通方程,熟练掌握参数方程与普通方程之间的转化是解本题的关键.

 执行如图的程序框图,若输入k=63,则输出的n=( )
执行如图的程序框图,若输入k=63,则输出的n=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 5 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
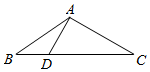 如图,已知点D在△ABC的BC边上,且∠DAC=90°,cosC=$\frac{\sqrt{6}}{3}$,AB=6,BD=$\sqrt{6}$,则ADsin∠BAD=.
如图,已知点D在△ABC的BC边上,且∠DAC=90°,cosC=$\frac{\sqrt{6}}{3}$,AB=6,BD=$\sqrt{6}$,则ADsin∠BAD=.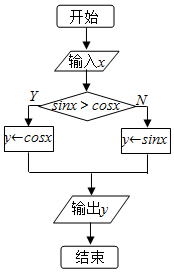 如图所示的流程图,若输出的x的值为$\frac{π}{3}$,则相应输出的y值为$\frac{1}{2}$.
如图所示的流程图,若输出的x的值为$\frac{π}{3}$,则相应输出的y值为$\frac{1}{2}$.