题目内容
19．
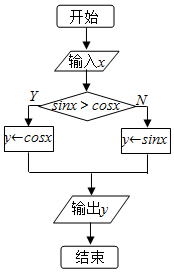如图所示的流程图，若输出的x的值为$\frac{π}{3}$，则相应输出的y值为$\frac{1}{2}$．
分析 由已知中的程序代码，可得该程序的功能是计算并输出分段函数y=$\left\{\begin{array}{l}{cosx}&{sinx＞cosx}\\{sinx}&{sinx≤cosx}\end{array}\right.$的值，由x的值为$\frac{π}{3}$，利用特殊角的三角函数值即可计算得解．
解答 解：由已知中的程序代码，可得该程序的功能是计算并输出分段函数y=$\left\{\begin{array}{l}{cosx}&{sinx＞cosx}\\{sinx}&{sinx≤cosx}\end{array}\right.$的值，
由于：sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$＞cos$\frac{π}{3}=\frac{1}{2}$，
所以：执行y=cos$\frac{π}{3}=\frac{1}{2}$，输出y的值为$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查了选择结构的程序框图，根据框图的流程判断算法的功能是关键，属于基础题．
练习册系列答案
相关题目
9．（2x+$\frac{1}{x}$）n的展开式的第三项系数与第四项系数相等，则二项式系数之和为（ ）
| A． | 128 | B． | 36 | C． | 256 | D． | 512 |
7．已知函数$f（x）=（{e^x}-\frac{1}{e^x}）{x^3}$，若实数a满足f（log2a）+f（log0.5a）≤2f（1），则实数a的取值范围是（ ）
| A． | $（-∞，\frac{1}{2}）∪（2，+∞）$ | B． | $（-∞，\frac{1}{2}]∪[2，+∞）$ | C． | $[\frac{1}{2}，2]$ | D． | $（\frac{1}{2}，2）$ |
11．一个车间为了规定工时定额，需要确定加工零件所花费时，为此进行了5次试验，测得的数据如下：
（I）如果y与x具有线性相关关系，求回归直线方程；
（Ⅱ）根据（I）所求回归直线方程，预测此车间加工这种件70个时，所需要的加工时间．
附：b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-{n\overline{x}}^{2}}$，$\overline{y}$=b$\overline{x}$+a．
| 零件数x（个） | 10 | 20 | 30 | 40 | 50 |
| 加工时间y（分钟） | 62 | 68 | 75 | 81 | 89 |
（Ⅱ）根据（I）所求回归直线方程，预测此车间加工这种件70个时，所需要的加工时间．
附：b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-{n\overline{x}}^{2}}$，$\overline{y}$=b$\overline{x}$+a．