题目内容
15.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,|$\overrightarrow{a}$|=$\sqrt{2}$,$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为1,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{4}$.分析 根据条件及一个向量在另一个向量方向上的投影的定义便可得到$\sqrt{2}cos<\overrightarrow{a},\overrightarrow{b}>=1$,从而有$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{\sqrt{2}}{2}$,这样根据向量夹角的范围便可得出$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的大小.
解答 解:∵$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为1,且$|\overrightarrow{a}|=\sqrt{2}$;
∴$|\overrightarrow{a}|cos<\overrightarrow{a},\overrightarrow{b}>=\sqrt{2}cos<\overrightarrow{a},\overrightarrow{b}>=1$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{\sqrt{2}}{2}$;
∴$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{4}$.
故答案为:$\frac{π}{4}$.
点评 考查一个向量在另一个向量方向上的投影的定义及计算公式,向量夹角的范围,以及已知三角函数值求角.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
3.执行如图所示的程序框图,输出的S的值为30,则输入的n为( )
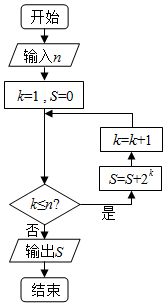

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
7.已知函数$f(x)=({e^x}-\frac{1}{e^x}){x^3}$,若实数a满足f(log2a)+f(log0.5a)≤2f(1),则实数a的取值范围是( )
| A. | $(-∞,\frac{1}{2})∪(2,+∞)$ | B. | $(-∞,\frac{1}{2}]∪[2,+∞)$ | C. | $[\frac{1}{2},2]$ | D. | $(\frac{1}{2},2)$ |