题目内容
2.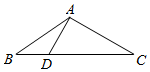 如图,已知点D在△ABC的BC边上,且∠DAC=90°,cosC=$\frac{\sqrt{6}}{3}$,AB=6,BD=$\sqrt{6}$,则ADsin∠BAD=.
如图,已知点D在△ABC的BC边上,且∠DAC=90°,cosC=$\frac{\sqrt{6}}{3}$,AB=6,BD=$\sqrt{6}$,则ADsin∠BAD=.
分析 由已知及$cosC=\frac{{\sqrt{6}}}{3}$,可得AC=$\frac{\sqrt{6}}{3}$CD,由余弦定理可解得CD,进而可求AC,即可得解sinB,由正弦定理即可计算ADsin∠BAD=BDsinB的值.
解答 解:∵∠DAC=90°,$cosC=\frac{{\sqrt{6}}}{3}$=$\frac{AC}{CD}$,可得:AC=$\frac{\sqrt{6}}{3}$CD,
又∵AB=6,$BD=\sqrt{6}$,
∴在△ABC中,由余弦定理可得:36=($\frac{\sqrt{6}}{3}$CD)2+($\sqrt{6}$+CD)2-2×$\frac{\sqrt{6}}{3}$CD×($\sqrt{6}$+CD)×$\frac{\sqrt{6}}{3}$,
∴整理可得:CD2+2$\sqrt{6}$CD-90=0,解得:CD=3$\sqrt{6}$,AC=6,
∵AB=AC=6,
∴sinB=sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{\sqrt{3}}{3}$,
∴在△ABD中,由正弦定理可得:ADsin∠BAD=BDsinB=$\sqrt{6}$×$\frac{\sqrt{3}}{3}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题主要考查了正弦定理,余弦定理,同角三角函数基本关系式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$均为单位向量,它们的夹角为$\frac{2π}{3}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
7.已知函数$f(x)=({e^x}-\frac{1}{e^x}){x^3}$,若实数a满足f(log2a)+f(log0.5a)≤2f(1),则实数a的取值范围是( )
| A. | $(-∞,\frac{1}{2})∪(2,+∞)$ | B. | $(-∞,\frac{1}{2}]∪[2,+∞)$ | C. | $[\frac{1}{2},2]$ | D. | $(\frac{1}{2},2)$ |
11.一个车间为了规定工时定额,需要确定加工零件所花费时,为此进行了5次试验,测得的数据如下:
(I)如果y与x具有线性相关关系,求回归直线方程;
(Ⅱ)根据(I)所求回归直线方程,预测此车间加工这种件70个时,所需要的加工时间.
附:b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-{n\overline{x}}^{2}}$,$\overline{y}$=b$\overline{x}$+a.
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 68 | 75 | 81 | 89 |
(Ⅱ)根据(I)所求回归直线方程,预测此车间加工这种件70个时,所需要的加工时间.
附:b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-{n\overline{x}}^{2}}$,$\overline{y}$=b$\overline{x}$+a.