题目内容
20.某大学自主招生考试面试环节中,共设置两类考题,A类题有4个不同的小题,B类题有6个不同的小题,某考生从中任抽取四道题解答.(Ⅰ)求该考生至少抽取到2道B类题的概率;
(Ⅱ)设所抽取的四道题中B类题的个数为X,求随机变量X的分布列与期望.
分析 (Ⅰ)设事件A:”该考生至少取到2道B类题”,利用对立事件概率计算公式能求出该考生至少抽取到2道B类题的概率.
(2)随机变量X的取值分别为0,1,2,3,4,分别求出相应的概率,由此能求出随机变量X的分布列与期望.
解答 解:(Ⅰ)设事件A:”该考生至少取到2道B类题”,
P(A)=$1-\frac{C_4^4+C_4^3C_6^1}{{C_{10}^4}}=\frac{37}{42}$.…(4分)
(2)随机变量X的取值分别为0,1,2,3,4,…(5分)
$P({X=0})=\frac{C_4^4}{{C_{10}^4}}=\frac{1}{210}$,$P({X=1})=\frac{C_4^3C_6^1}{{C_{10}^4}}=\frac{24}{210}$,$P({X=2})=\frac{C_4^2C_6^2}{{C_{10}^4}}=\frac{90}{210}$,
$P({X=3})=\frac{C_4^1C_6^3}{{C_{10}^4}}=\frac{80}{210}$,$P({X=4})=\frac{C_6^4}{{C_{10}^4}}=\frac{15}{210}$,…(10分)
∴随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{210}$ | $\frac{24}{210}$ | $\frac{90}{210}$ | $\frac{80}{210}$ | $\frac{15}{210}$ |
∴随机变量X的期望为:$EX=0×\frac{1}{210}+1×\frac{24}{210}+2×\frac{90}{210}+3×\frac{80}{210}+4×\frac{15}{210}=\frac{12}{5}$.…(13分)
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
8.执行如图所示的程序框图,若输入的x,y,k分别为1,2,3,则输出的N=( )
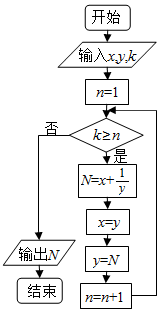

| A. | $\frac{3}{2}$ | B. | $\frac{15}{8}$ | C. | $\frac{16}{5}$ | D. | $\frac{8}{3}$ |
9.(2x+$\frac{1}{x}$)n的展开式的第三项系数与第四项系数相等,则二项式系数之和为( )
| A. | 128 | B. | 36 | C. | 256 | D. | 512 |
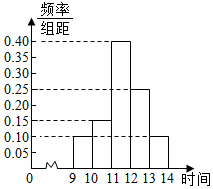 某商场在庆元宵节促销活动中,对元宵节9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售额为10万元.
某商场在庆元宵节促销活动中,对元宵节9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售额为10万元.