题目内容
关于x方程
-x=lnx有唯一的解，则实数a的取值范围是 ．
| x2 |
| a |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：根据方程和函数之间的关系，将方程转化为两个函数，利用数形结合即可得到结论．
解答：
解：要使方程有意义，则x＞0，
设f（x）=
-x，g（x）=lnx，
若a＜0，此时函数f（x）在x＞0时，单调递减，g（x）=lnx单调递增，
此时两个函数只有一个交点，满足方程有唯一解；
若a＞0，要使方程
-x=lnx有唯一的解，
则f（x）与g（x）在（1，0）处相切，
即此时f（1）=0，即a=1，满足条件．
故答案为：{a|a＜0或a=1}
设f（x）=
| x2 |
| a |
若a＜0，此时函数f（x）在x＞0时，单调递减，g（x）=lnx单调递增，
此时两个函数只有一个交点，满足方程有唯一解；
若a＞0，要使方程
| x2 |
| a |
则f（x）与g（x）在（1，0）处相切，
即此时f（1）=0，即a=1，满足条件．
故答案为：{a|a＜0或a=1}
点评：本题主要考查函数交点个数的应用，将方程转化为函数，利用数形结合是解决本题的关键，本题综合性较强，有一定的难度．
练习册系列答案
相关题目
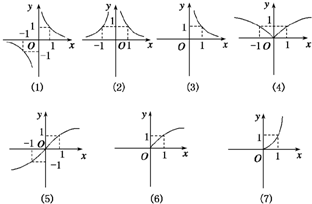
为了了解广东人的生活幸福指数，对40到60岁中年人一天的运动时间（单位：t），现随机地选出50名做调查，下表是一天运动时间频率分布表：给定一组函数解析式：①y=x
；②y=x
；③y=x-
；④y=x-
；⑤y=x
；⑥y=x-
；⑦y=x
，如图所示一组函数图象．图象对应的解析式号码顺序正确的是（ ）
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、⑥③④②⑦①⑤ |
| B、⑥④②③⑦①⑤ |
| C、⑥④③②⑦①⑤ |
| D、⑥④③②⑦⑤① |