题目内容
求函数y=
+x2的最小值．
| 9 |
| 4(1+4x2) |
考点：函数的值域,基本不等式
专题：不等式
分析：把解析式进行变形，利用基本不等式的性质求出最小值，注意等号成立的条件．
解答：
解：函数y=
+x2=
+(x2+
)-
≥2
-
=
，
当(
+x2)=
，即x=±
时，等号成立．
∴y≥
，即函数的最小值为
．
| 9 |
| 4(1+4x2) |
| ||
|
| 1 |
| 4 |
| 1 |
| 4 |
|
| 1 |
| 4 |
| 5 |
| 4 |
当(
| 1 |
| 4 |
| ||
|
| ||
| 2 |
∴y≥
| 5 |
| 4 |
| 5 |
| 4 |
点评：运用基本不等式解题时注意成立的条件：一正，二定，三相等．
练习册系列答案
名校课堂系列答案
相关题目
给定一组函数解析式：①y=x
；②y=x
；③y=x-
；④y=x-
；⑤y=x
；⑥y=x-
；⑦y=x
，如图所示一组函数图象．图象对应的解析式号码顺序正确的是（ ）
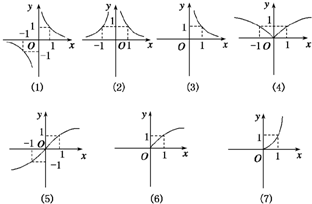
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、⑥③④②⑦①⑤ |
| B、⑥④②③⑦①⑤ |
| C、⑥④③②⑦①⑤ |
| D、⑥④③②⑦⑤① |