题目内容
一个几何体的三视图如图所示（单位：cm），则该几何体的体积为（ ）
A、（32+
| ||
B、（32+
| ||
C、（41+
| ||
D、（41+
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体是两个正四棱柱与一个圆柱的组合体，根据三视图判断正四棱柱的底面边长和高及圆柱的底面直径和高的数据，代入圆锥与棱柱的体积公式计算．
解答：
解：由三视图知：几何体是两个正四棱柱与一个圆柱的组合体，
其中圆柱的底面直径为1，高为1；
上边正四棱柱的底面边长为3，高为1；
下边正四棱柱的底面边长为4，高为2，
∴几何体的体积V=32×1+42×2+π×(
)2×1=（41+
）cm3．
故选：C．
其中圆柱的底面直径为1，高为1；
上边正四棱柱的底面边长为3，高为1；
下边正四棱柱的底面边长为4，高为2，
∴几何体的体积V=32×1+42×2+π×(
| 1 |
| 2 |
| π |
| 4 |
故选：C．
点评：本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及数据所对应的几何量是解答此类问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
给定一组函数解析式：①y=x
；②y=x
；③y=x-
；④y=x-
；⑤y=x
；⑥y=x-
；⑦y=x
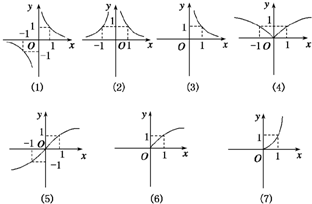
，如图所示一组函数图象．图象对应的解析式号码顺序正确的是（ ）
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、⑥③④②⑦①⑤ |
| B、⑥④②③⑦①⑤ |
| C、⑥④③②⑦①⑤ |
| D、⑥④③②⑦⑤① |
甲、乙、丙三人投掷飞镖，他们的成绩（环数）如图频数条形统计图所示．则甲、乙、丙三人训练成绩方差s甲2，s乙2，s丙2的大小关系是（ ）
| A、s丙2＜s乙2＜s甲2 |
| B、s丙2＜s甲2＜s乙2 |
| C、s甲2＜s丙2＜s乙2 |
| D、s乙2＜s丙2＜s甲2 |
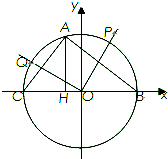如图，已知B、C是以原点O为圆心，半径为1的圆与x轴的交点，点A在劣弧 |
| PQ |
| AH |
| AB |
| AC |
A、(0，
| ||||
B、[
| ||||
C、[
| ||||
D、[
|