题目内容
“
”称为a,b,c三个正实数的“调和平均数”,若正数x,y满足“x,y,xy的调和平均数为3”,则x+2y的最小值是( )
| 3 | ||||||
|
| A、3 | B、5 | C、7 | D、8 |
考点:基本不等式
专题:综合题,不等式的解法及应用
分析:由调和平均数的定义,结合已知得到x=
,再由x>0得到y>1,把x=
代入x+2y,整理后利用基本不等式求最值.
| y+1 |
| y-1 |
| y+1 |
| y-1 |
解答:
解:由“调和平均数”定义知,
x,y,xy的调和平均数为
=3,
整理得:x+y+1=xy,x=
,
∵x=
>0,
∴y>1.
则x+2y=
+2y=
=
=
=2(y-1)+
+3≥2
+3=7.
当且仅当2(y-1)=
,即y=2时上式等号成立.
∴x+2y的最小值是7.
故选:C.
x,y,xy的调和平均数为
| 3 | ||||||
|
整理得:x+y+1=xy,x=
| y+1 |
| y-1 |
∵x=
| y+1 |
| y-1 |
∴y>1.
则x+2y=
| y+1 |
| y-1 |
| y+1+2y2-2y |
| y-1 |
| 2y2-y+1 |
| y-1 |
=
| 2(y-1)2+3(y-1)+2 |
| y-1 |
| 2 |
| y-1 |
2(y-1)•
|
当且仅当2(y-1)=
| 2 |
| y-1 |
∴x+2y的最小值是7.
故选:C.
点评:本题考查了基本不等式求最值,在利用调和平均数的定义结合已知得到x、y的关系后,关键在于整理变形,使得要求最小值的式子能利用基本不等式求解,是中档题.

练习册系列答案
相关题目
设集合U={x∈N*|x≤4},A={1,2},B={2,4},则(∁UA)∪B=( )
| A、{1,2} |
| B、{1,2,3,4} |
| C、{3,4} |
| D、{2,3,4} |
给定一组函数解析式:①y=x
;②y=x
;③y=x-
;④y=x-
;⑤y=x
;⑥y=x-
;⑦y=x
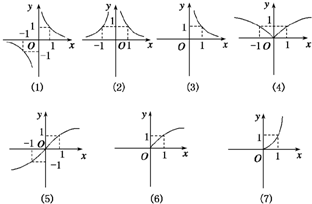
,如图所示一组函数图象.图象对应的解析式号码顺序正确的是( )
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |

| A、⑥③④②⑦①⑤ |
| B、⑥④②③⑦①⑤ |
| C、⑥④③②⑦①⑤ |
| D、⑥④③②⑦⑤① |
若按如图的算法流程图运行后,输出的结果是
,则输入的N的值为( )

| 6 |
| 7 |

| A、5 | B、6 | C、7 | D、8 |
甲、乙、丙三人投掷飞镖,他们的成绩(环数)如图频数条形统计图所示.则甲、乙、丙三人训练成绩方差s甲2,s乙2,s丙2的大小关系是( )


| A、s丙2<s乙2<s甲2 |
| B、s丙2<s甲2<s乙2 |
| C、s甲2<s丙2<s乙2 |
| D、s乙2<s丙2<s甲2 |