题目内容
11.已知O为△ABC的外心,且$|{\overrightarrow{AB}}|=7,|{\overrightarrow{AC}}|=5$,则$\overrightarrow{AO}•\overrightarrow{BC}$的值为-12.分析 过O分别作OE⊥AB,OF⊥AC,垂足分别为E,F.利用垂经定理及数量积的运算性质可得$\overrightarrow{AO}$•$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AB}$2,$\overrightarrow{AO}$•$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{AC}$2.再利用向量的三角形法则、数量积的运算性质即可得出.
解答 解:如图所示,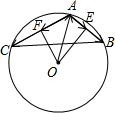
过O分别作OE⊥AB,OF⊥AC,垂足分别为E,F.
∴$\overrightarrow{AO}$•$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AB}$2,$\overrightarrow{AO}$•$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{AC}$2.
∴$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\overrightarrow{AO}$•($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\overrightarrow{AO}$•$\overrightarrow{AC}$-$\overrightarrow{AO}$•$\overrightarrow{AB}$
=$\frac{1}{2}$$\overrightarrow{AC}$2-$\frac{1}{2}$$\overrightarrow{AB}$2=$\frac{1}{2}$×(52-72)=-12.
故答案为:-12.
点评 本题考查了三角形的外心性质、垂径定理、向量的三角形法则及数量积的运算性质,考查了推理能力与计算能力,属于中档题.

| A. | 4 | B. | 9 | C. | 10 | D. | 18 |
| A. | $\frac{10}{3}$ | B. | 一$\frac{10}{3}$ | C. | $\frac{10}{13}$ | D. | 一$\frac{10}{13}$ |
| A. | $\frac{π}{4}$ | B. | $\frac{π}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{16}$ |