题目内容
5.记函数f(x)=-2m+2msin(x+$\frac{3π}{2}$)-2cos2(x-$\frac{π}{2}$)+1,x∈[-$\frac{π}{2}$,0]的最小值为h(m).(1)求h(m);
(2)若h(m)=$\frac{1}{2}$,求m及此时f(x)的最大值.
分析 (1)把函数f(x)化成关于cosx的函数,利用换元法把问题转化为二次函数的问题,讨论对称轴的位置,求出函数f(x)的最小值h(m);
(2)根据分段函数h(m)=$\frac{1}{2}$,求出对应m的值,计算f(x)的最大值.
解答 解:(1)函数f(x)=-2m+2msin(x+$\frac{3π}{2}$)-2cos2(x-$\frac{π}{2}$)+1
=-2m-2mcosx-2sin2x+1
=-2m-2mcosx-2(1-cos2x)+1
=2cos2x-2mcosx-2m-1,
又x∈[-$\frac{π}{2}$,0],
∴cosx∈[0,1],
令t=cosx,则0≤t≤1,
则函数f(t)=2t2-2mt-2m-1,且对称轴为t=$\frac{m}{2}$;
当0≤$\frac{m}{2}$≤1,即0≤m≤2时,
f(t)min=f($\frac{m}{2}$)=-$\frac{{m}^{2}}{2}$-2m-1;
当$\frac{m}{2}$>1,即m>2时,
f(t)min=f(1)=-4m+1;
当$\frac{m}{2}$<0,即m<0时,
f(t)min=f(0)=-2m-1;
综上,f(x)的最小值是
h(m)=$\left\{\begin{array}{l}{-4m+1,m>2}\\{-\frac{{m}^{2}}{2}-2m-1,0≤m≤2}\\{-2m-1,m<0}\end{array}\right.$;
(2)若h(m)=$\frac{1}{2}$,则m>2时,-4m+1=$\frac{1}{2}$,
解得m=$\frac{1}{8}$,不满足条件,舍去;
0≤m≤2时,-$\frac{{m}^{2}}{2}$-2m-1=$\frac{1}{2}$,
解得m=-1或m=-3,不满足条件,舍去;
m<0时,-2m-1=$\frac{1}{2}$,解得m=-$\frac{3}{4}$;
综上,m=-$\frac{3}{4}$;
此时f(t)=2t2+$\frac{3}{2}$t+$\frac{1}{2}$在t∈[0,1]上单调递增,
∴f(x)的最大值是f(1)=2+$\frac{3}{2}$+$\frac{1}{2}$=4.
点评 本题主要考查了三角函数的最值问题,一般的方法是转化为二次函数的问题,利用二次函数的性质求得最值,是综合题.

| 日期 | 2月1日 | 2月2日 | 2月3日 | 2月4日 | 2月5日 |
| 温差x(°C) | 10 | 11 | 13 | 12 | 8 |
| 发芽数x(颗) | 23 | 25 | 30 | 26 | 16 |
(Ⅰ)求选取的2组数据恰好是不相邻的2天数据的概率;
(Ⅱ)若选取的是2月1日与2月5日的两组数据,请根据2月2日至2月4日的数据,求出y关于x的线性回归方程
$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;可以预报当温差为20℃时,种子发芽数.
附:回归直线方程:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$;$\stackrel{∧}{b}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| A. | 5 | B. | 8 | C. | $\sqrt{17}-1$ | D. | $\sqrt{15}-1$ |
| A. | $\frac{π}{2}$ | B. | Π | C. | 2π | D. | 3π |
| A. | $\frac{5}{8}$ | B. | $\frac{13}{16}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
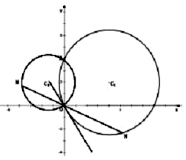 已知圆${C_1}:{({x-4})^2}+{({y-2})^2}=20$与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;
已知圆${C_1}:{({x-4})^2}+{({y-2})^2}=20$与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;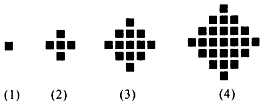 某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.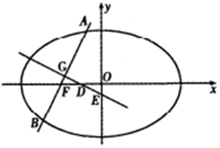 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),过点F的直线交椭圆于A,B两点,当直线AB经过椭圆的一个顶点时,其倾斜角恰为60°.
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),过点F的直线交椭圆于A,B两点,当直线AB经过椭圆的一个顶点时,其倾斜角恰为60°.