题目内容
15.已知函数f(x)=x2+mx+n,其中1≤m≤3,0≤n≤4,记函数f(x)满足条件$\left\{\begin{array}{l}f(2)≤12\\ f(-1)≤3\end{array}\right.$的事件为A,则事件A发生的概率为( )| A. | $\frac{5}{8}$ | B. | $\frac{13}{16}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
分析 根据二次函数解析式,可得事件A对应的不等式为$\left\{\begin{array}{l}{2m+n≤8}\\{-m+n≤2}\end{array}\right.$,因此在同一坐标系内作出不等式组1≤m≤4,0≤n≤4和可得$\left\{\begin{array}{l}{2m+n≤8}\\{-m+n≤2}\end{array}\right.$对应的平面区域,分别得到矩形ABCD和影音部分的面积,即可得到事件A发生的概率.
解答 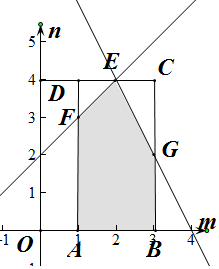 解:∵f(x)=x2+mx+n,
解:∵f(x)=x2+mx+n,
∴不等式$\left\{\begin{array}{l}f(2)≤12\\ f(-1)≤3\end{array}\right.$,可得$\left\{\begin{array}{l}{2m+n≤8}\\{-m+n≤2}\end{array}\right.$
以m为横坐标、n为纵坐标建立直角坐标系,
将不等式1≤m≤3,0≤n≤4和$\left\{\begin{array}{l}{2m+n≤8}\\{-m+n≤2}\end{array}\right.$对应的平面区域作出,如图所示
不等式组1≤m≤4,0≤n≤4对应图中的矩形ABCD,
其中A(1,0),B(3,0),C(3,4),D(1,4),E(2,4),F(1,3),G(3,2)
可得S矩形ABCD=2×4=8,S△DEF=$\frac{1}{2}$×1×1=$\frac{1}{2}$,S△ECG=$\frac{1}{2}$×1×2=1,
对应图中的阴影部分的面积为=S矩形ABCD-S△DEF-S△ECG=8-$\frac{1}{2}$-1=$\frac{13}{2}$
∴事件A发生的概率为P(A)=$\frac{\frac{13}{2}}{8}$=$\frac{13}{16}$
故选B.
点评 本题以二次函数与不等式的运算为载体,求事件A发生的概率.着重考查了二元一次不等式组表示的平面区域和几何概型计算公式等知识,属于中档题.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案| A. | 充分条件 | B. | 必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 0.28J | B. | 0.12J | C. | 0.26J | D. | 0.18J |
| A. | “sinα=$\frac{3}{5}$”是“cos2α=$\frac{7}{25}$”的必要不充分条件 | |
| B. | 命题“若xy=0,则x=0或y=0”的否命题是“若xy≠0,则x≠0或y≠0” | |
| C. | 已知命题p:?x∈R,使2x>3x;命题q:?x∈(0,+∞),都有$\frac{1}{{x}^{2}}$<$\frac{1}{{x}^{3}}$,则p∧(¬q)是真命题 | |
| D. | 从匀速传递的生产流水线上,质检员每隔5分钟从中抽取一件产品进行某项指标检测,这是分层抽样 |
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分又不必要条件 |
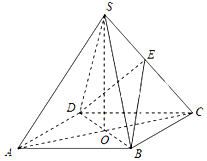 如图,在四棱锥S-ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC的中点.