题目内容
已知函数f(x)=2cosx•sin(
+x)(x∈R)
(1)求f(x)在[0,π]上的单调增区间;
(2)△ABC中,f(C)=1,且边长c=2,求△ABC面积的最大值.
| π |
| 6 |
(1)求f(x)在[0,π]上的单调增区间;
(2)△ABC中,f(C)=1,且边长c=2,求△ABC面积的最大值.
考点:三角函数中的恒等变换应用,正弦定理
专题:常规题型,三角函数的图像与性质,解三角形
分析:第(1)问求三角函数的单调区间,要先把函数化成y=Asin(ωx+φ)+B的形式,然后再根据正弦函数的单调区间求解;第(2)问根据f(C)=1求出角C,然后利用面积公式写出面积表达式,结合余弦定理和基本不等式求三角形面积的最大值.
解答:
解:(1)f(x)=2cosx•sin(
+x)
=2cosx(
cosx+
sinx)
=cos2x+
sinxcosx
=
+
sin2x
=-sin(2x+
)+
由
+2kπ≤2x+
≤
+2kπ(k∈Z)
得
+kπ≤x≤
+kπ(k∈Z)
∵x∈[0,π]
所以函数f(x)在[0,π]上的单调增区间为[
,
].
(2)由f(C)=-sin(2C+
)+
=1得
sin(2c+
)=-
,解得C=
或C=
∵S=
absinC
又∵cosC=
要使面积取到最大值,则C=
,
所以a2+b2=4,所以ab≤2,
所以Smax=
×2×1=1.
| π |
| 6 |
=2cosx(
| 1 |
| 2 |
| ||
| 2 |
=cos2x+
| 3 |
=
| 1+cos2x |
| 2 |
| ||
| 2 |
=-sin(2x+
| π |
| 6 |
| 1 |
| 2 |
由
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
得
| π |
| 6 |
| 2π |
| 3 |
∵x∈[0,π]
所以函数f(x)在[0,π]上的单调增区间为[
| π |
| 6 |
| 2π |
| 3 |
(2)由f(C)=-sin(2C+
| π |
| 6 |
| 1 |
| 2 |
sin(2c+
| π |
| 6 |
| 1 |
| 2 |
| π |
| 2 |
| 5π |
| 6 |
∵S=
| 1 |
| 2 |
又∵cosC=
| a2+b2-4 |
| 2ab |
要使面积取到最大值,则C=
| π |
| 2 |
所以a2+b2=4,所以ab≤2,
所以Smax=
| 1 |
| 2 |
点评:本题考查了求三角函数的单调区间,关键是利用三角恒等变换化成标准形式;求三角形面积的最大值,关键是选择适当的面积公式结合正、余弦定理和基本不等式进行求解.

练习册系列答案
相关题目
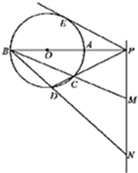 如图,已知PE是⊙O的切线,切点为E,PAB,PCD都是⊙O的割线,且PAB经过圆心O,过点P直线与直线BC,BD分别交于点M,N,且PE2=PM•PN.
如图,已知PE是⊙O的切线,切点为E,PAB,PCD都是⊙O的割线,且PAB经过圆心O,过点P直线与直线BC,BD分别交于点M,N,且PE2=PM•PN.