题目内容
若f(x)=
x3-4x+2与直线y=k有且只有一个交点,则k的取值范围为 .
| 1 |
| 3 |
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:将题中条件:“函数f(x)的图象与直线y=k只有一个公共点,”等价于“g(x)=f(x)-k,所以g(x)只有一个零点”,利用导数求得原函数的极值,最后要使g(x)的其图象和x轴只有一个交点,得到关于k的不等关系,从而求实数k的取值范围.
解答:
解:令g(x)=f(x)-k,所以g(x)只有一个零点,
因为g′(x)=f′(x)=x2-4
所以令g′(x)=0,解得x=2或x=-2,
所以情况如下表:
g(x)有且仅有一个零点等价于g(-2)<0或g(2)>0,
所以-
+8+2-k<0或
-8+2-k>0,解得k>
或k<-
.
故答案为:k>
或k<-
.
因为g′(x)=f′(x)=x2-4
所以令g′(x)=0,解得x=2或x=-2,
所以情况如下表:
| x | (-∞,-2) | -2 | (-2,2) | 2 | (2,+∞) |
| g′(x) | + | 0 | - | 0 | + |
| g(x) | 增 | 极大值 | 减 | 极小值 | 增 |
所以-
| 8 |
| 3 |
| 8 |
| 3 |
| 22 |
| 3 |
| 10 |
| 3 |
故答案为:k>
| 22 |
| 3 |
| 10 |
| 3 |
点评:本小题主要考查导数在极值问题中的应用、不等式的解法等基础知识,考查运算求解能力,转化思想.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
命题“?x>0,x2+3x+2≥0”的否定是( )
| A、?x≤0,x2+3x+2≥0 |
| B、?x≤0,x2+3x+2<0 |
| C、?x>0,x2+3x+2≥0 |
| D、?x>0,x2+3x+2<0 |
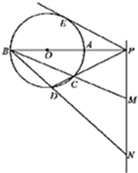 如图,已知PE是⊙O的切线,切点为E,PAB,PCD都是⊙O的割线,且PAB经过圆心O,过点P直线与直线BC,BD分别交于点M,N,且PE2=PM•PN.
如图,已知PE是⊙O的切线,切点为E,PAB,PCD都是⊙O的割线,且PAB经过圆心O,过点P直线与直线BC,BD分别交于点M,N,且PE2=PM•PN.