题目内容
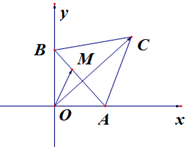如图，边长为2的正三角形ABC的两个顶点A，B分别在x，y轴的正半轴上滑动，| AM |
| MB |
| OM |
| OC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：设∠OAB=θ，θ∈(0，
)．可得A（2cosθ，0），B（0，2sinθ），C（2sin（30°+θ），2sin（60°+θ））．利用
=2
，可得
=
，
=(
cosθ，
sinθ)．
于是
•
=
cosθsin(30°+θ)+
sinθsin(60°+θ)展开化简即可得出．
| π |
| 2 |
| AM |
| MB |
| AM |
| 2 |
| 3 |
| AB |
| OM |
| 2 |
| 3 |
| 4 |
| 3 |
于是
| OM |
| OC |
| 4 |
| 3 |
| 8 |
| 3 |
解答：
解：设∠OAB=θ，θ∈(0，
)．
则A（2cosθ，0），B（0，2sinθ），C（2cosθ-2cos（60°+θ），2sin（60°+θ））即（2sin（30°+θ），2sin（60°+θ））．
∵
=2
，∴
=
，
∴
=
+
(
-
)=
+
=(
cosθ，
sinθ)．
∴
•
=
cosθsin(30°+θ)+
sinθsin(60°+θ)
=
sin2θ-
cos2θ+1
=
sin(2θ-φ)+1≤
+1，当且仅当sin（2θ-φ）=1时去等号．
故最大值为：1+
．
| π |
| 2 |
则A（2cosθ，0），B（0，2sinθ），C（2cosθ-2cos（60°+θ），2sin（60°+θ））即（2sin（30°+θ），2sin（60°+θ））．
∵
| AM |
| MB |
| AM |
| 2 |
| 3 |
| AB |
∴
| OM |
| OA |
| 2 |
| 3 |
| OB |
| OA |
| 1 |
| 3 |
| OA |
| 2 |
| 3 |
| OB |
| 2 |
| 3 |
| 4 |
| 3 |
∴
| OM |
| OC |
| 4 |
| 3 |
| 8 |
| 3 |
=
| 3 |
| 1 |
| 3 |
=
2
| ||
| 3 |
2
| ||
| 3 |
故最大值为：1+
2
| ||
| 3 |
点评：本题考查了向量的坐标运算、数量积运算、三角函数的化简、正弦函数的单调性有界性等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
用红、黄、蓝、绿、黑5种颜色给如图的a、b、c、d四个区域染色，若相邻的区域不能用相同的颜色，不同的染色方法的种数有既在区间（0，
）上是增函数又是以π为周期的偶函数的是（ ）
| π |
| 2 |
| A、y=|cosx| |
| B、y=sin|x| |
| C、y=cos2x |
| D、y=|sinx| |