题目内容

定义运算a⊕b=
a，a≥b
b，a＜b
，则关于正实数x的不等式4⊕（x+
4
x
）＜5⊕（2x）的解集为
 
．
考点：其他不等式的解法
专题：不等式的解法及应用
分析：由新定义可得分段不等式，结合函数图象可得．
解答： 解：∵a⊕b=
a，a≥b
b，a＜b
，
∴4⊕（x+
4
x
）=
4，x=2
x+
4
x
，x＞0且x≠2
，
同理可得5⊕（2x）=
5，0＜x≤
5
2
2x，x＞
5
2
，
∴不等式4⊕（x+
4
x
）＜5⊕（2x）的解集为：（1，+∞）
故答案为：（1，+∞）
点评：本题考查不等式的解集，涉及新定义，属基础题．
练习册系列答案
相关题目
命题“若p则q”的逆命题是
 
．
长为10cm的线段AB上有一点C，则C与A、B的距离均大于2cm的概率为
 
．
若log
3
4
a＞1，则实数a的取值范围是
 
．
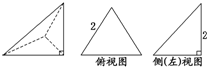已知三棱锥的直观图及其俯视图与侧（左）视图如图，俯视图是边长为2的正三角形，侧（左）视图是有一直角边为2的直角三角形，则该三棱锥的正（主）视图面积为
 
．
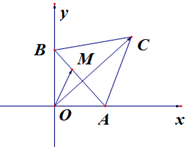随机抽取某校甲、乙两个班各10名同学，测量他们的身高（单位：cm）后获得身高数据的茎叶图如图所示，在这20人中，记身高在[150，160），[160，170），[170，180），[180，190）的人数依次为A1，A2，A3，A4，则框图中输出的数据为
 
．
如图，边长为2的正三角形ABC的两个顶点A，B分别在x，y轴的正半轴上滑动，
AM
=2
MB
，求
OM
•
OC
的最大值是
 
．
将函数y=f（x）的图象上的每一点的纵坐标变为原来的2倍，横坐标变为原来的2倍，然后把所得的图象上的所有点沿x轴向左平移
π
6
个单位，这样得到的曲线和函数y=sin2x的图象相同，则函数y=f（x）的解析式为
 
．
已知函数f（x）=sinxcosx+1，将f（x）的图象向左平移
π
6
个单位得到函数g（x）的图象，则函数g（x）的单调减区间为（　　）
A、[
π
12
+2kπ，
7π
12
+2kπ]，k∈Z
B、[
π
12
+kπ，
7π
12
+kπ]，k∈Z
C、[
π
6
+kπ，
2π
3
+kπ]，k∈Z
D、[
π
6
+2kπ，
2π
3
+2kπ]，k∈Z

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网