题目内容
已知实数x，y满足
，则z=x-y的最小值为 ．
|
考点：简单线性规划
专题：不等式的解法及应用
分析：作出可行域，平移目标直线可得最优解，代值计算可得．
解答：
解：由题意可作出可行域（图中阴影三角形），
变形目标函数为y=x-z，
平邑目标直线（红色虚线），
可知当直线经过图中点A（0，3）时，目标函数取最小值，
代入计算可得z=x-y的最小值为=-3=-3
故答案为：-3
解：由题意可作出可行域（图中阴影三角形），变形目标函数为y=x-z，
平邑目标直线（红色虚线），
可知当直线经过图中点A（0，3）时，目标函数取最小值，
代入计算可得z=x-y的最小值为=-3=-3
故答案为：-3
点评：本题考查线性规划，作图是解决问题的关键，属基础题．
练习册系列答案
高中必刷题系列答案
相关题目
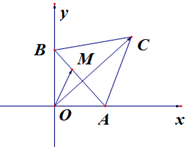如图，边长为2的正三角形ABC的两个顶点A，B分别在x，y轴的正半轴上滑动，
已知集合A={-1，0，1，2，3}，B={x∈R|
＜2}，则A∩B=（ ）
| 3 |
| x |
| A、{1，2，3} |
| B、{2，3} |
| C、{-1，2，3} |
| D、{-1，1，2} |