题目内容
 用红、黄、蓝、绿、黑5种颜色给如图的a、b、c、d四个区域染色,若相邻的区域不能用相同的颜色,不同的染色方法的种数有
用红、黄、蓝、绿、黑5种颜色给如图的a、b、c、d四个区域染色,若相邻的区域不能用相同的颜色,不同的染色方法的种数有考点:排列、组合及简单计数问题
专题:应用题,排列组合
分析:由于规定一个区域只涂一种颜色,相邻的区域颜色不同,可分步进行,区域a有5种涂法,b有4种涂法,c有3种,d有3种涂法,根据乘法原理可得结论.
解答:
解:由题意,由于规定一个区域只涂一种颜色,相邻的区域颜色不同,可分步进行,
区域a有5种涂法,b有4种涂法,c有3种,d有3种涂法
∴共有5×4×3×3=180种不同的染色方法.
故答案为:180.
区域a有5种涂法,b有4种涂法,c有3种,d有3种涂法
∴共有5×4×3×3=180种不同的染色方法.
故答案为:180.
点评:本题以实际问题为载体,考查计数原理的运用,关键搞清是分类,还是分步.

练习册系列答案
相关题目
“x=2kπ+
(k∈Z)”是“|sinx|=1”的( )
| π |
| 2 |
| A、充分非必要条件 |
| B、必要分充分条件 |
| C、充要条件 |
| D、即非充分又非必要条件 |
 已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的上底面面积是
已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的上底面面积是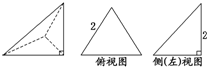 已知三棱锥的直观图及其俯视图与侧(左)视图如图,俯视图是边长为2的正三角形,侧(左)视图是有一直角边为2的直角三角形,则该三棱锥的正(主)视图面积为
已知三棱锥的直观图及其俯视图与侧(左)视图如图,俯视图是边长为2的正三角形,侧(左)视图是有一直角边为2的直角三角形,则该三棱锥的正(主)视图面积为
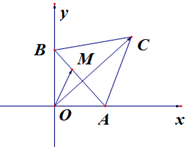 如图,边长为2的正三角形ABC的两个顶点A,B分别在x,y轴的正半轴上滑动,
如图,边长为2的正三角形ABC的两个顶点A,B分别在x,y轴的正半轴上滑动,