题目内容
已知a＞0，b＞0，
+
=1，则a+b的最小值是 ．
| 1 |
| 2a+b |
| 1 |
| b+1 |
考点：基本不等式
专题：计算题,不等式的解法及应用
分析：由
+
=1，得2a=1+
-b，则2a+2b=1+
+b，利用基本不等式即可求得．
| 1 |
| 2a+b |
| 1 |
| b+1 |
| 1 |
| b |
| 1 |
| b |
解答：
解：由
+
=1，得2a=1+
-b，
∴2a+2b=1+
+b≥1+2
=3，当且仅当b=1时取等号，
∴a+b≥
，即a+b的最小值为
，
故答案为：
．
| 1 |
| 2a+b |
| 1 |
| b+1 |
| 1 |
| b |
∴2a+2b=1+
| 1 |
| b |
|
∴a+b≥
| 3 |
| 2 |
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
点评：该题考查利用基本不等式求函数的最值，属基础题，注意适用条件：一正、二定、三相等．
练习册系列答案
相关题目
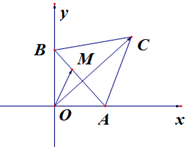如图，边长为2的正三角形ABC的两个顶点A，B分别在x，y轴的正半轴上滑动，