题目内容
既在区间(0,
)上是增函数又是以π为周期的偶函数的是( )
| π |
| 2 |
| A、y=|cosx| |
| B、y=sin|x| |
| C、y=cos2x |
| D、y=|sinx| |
考点:三角函数的周期性及其求法,正弦函数的单调性
专题:三角函数的图像与性质
分析:根据三角函数的周期性、单调性、奇偶性,得出结论.
解答:
解:由于y=|cosx|在区间(0,
)上是减函数,故排除A.
由y=sin|x|的图象可得,函数不是周期函数,故排除B.
由于y=cos2x在区间(0,
)上是减函数,故排除C.
由于y=|sinx|在区间(0,
)上是增函数,又是以π为周期的偶函数,故满足条件,
故选:D.
| π |
| 2 |
由y=sin|x|的图象可得,函数不是周期函数,故排除B.
由于y=cos2x在区间(0,
| π |
| 2 |
由于y=|sinx|在区间(0,
| π |
| 2 |
故选:D.
点评:本题主要考查三角函数的周期性、单调性、奇偶性,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=sinxcosx+1,将f(x)的图象向左平移
个单位得到函数g(x)的图象,则函数g(x)的单调减区间为( )
| π |
| 6 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
“x=2kπ+
(k∈Z)”是“|sinx|=1”的( )
| π |
| 2 |
| A、充分非必要条件 |
| B、必要分充分条件 |
| C、充要条件 |
| D、即非充分又非必要条件 |
已知集合A={-1,0,1,2,3},B={x∈R|
<2},则A∩B=( )
| 3 |
| x |
| A、{1,2,3} |
| B、{2,3} |
| C、{-1,2,3} |
| D、{-1,1,2} |
i是虚数单位,复数
的虚部是( )
| 1-3i |
| 1-i |
| A、-1 | B、-i | C、-2 | D、-2i |
设抛物线C:y2=3px(p≥0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,3),则C的方程为( )
| A、y2=4x或y2=8x |
| B、y2=2x或y2=8x |
| C、y2=4x或y2=16x |
| D、y2=2x或y2=16x |
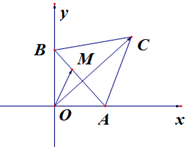 如图,边长为2的正三角形ABC的两个顶点A,B分别在x,y轴的正半轴上滑动,
如图,边长为2的正三角形ABC的两个顶点A,B分别在x,y轴的正半轴上滑动,