题目内容
定长为l﹙l＞
﹚的线段AB的端点在双曲线b2x2-a2y2=a2b2的右支上，则AB中点M的横坐标的最小值为 ．
| 2b2 |
| a |
考点：双曲线的简单性质
专题：计算题,圆锥曲线中的最值与范围问题
分析：用A、B 两点的坐标表示出|FA|和|FB|，解出A、B 两点的坐标，利用（|FA|+|FB|）≥|AB|，求得m的最小值．
解答：
解：设AB中点M的横坐标为m，则
|FA|=e（xA-
），|FB|=e（xB-
），
∴m=
•
（|FA|+|FB|）+
≥
|AB|+
=
+
=
+
当且仅当F、A、B共线时，m取得最小值．
故答案为：
+
．
|FA|=e（xA-
| a2 |
| c |
| a2 |
| c |
∴m=
| 1 |
| 2 |
| 1 |
| e |
| a2 |
| c |
≥
| 1 |
| 2e |
| a2 |
| c |
| l |
| 2e |
| a2 |
| c |
| la |
| 2c |
| a2 |
| c |
当且仅当F、A、B共线时，m取得最小值．
故答案为：
| la |
| 2c |
| a2 |
| c |
点评：本题考查双曲线的定义和双曲线的标准方程，基本不等式、以及双曲线的简单性质的应用，属于中档题．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
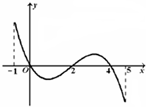已知函数y=f（x）的定义域为[-1，5]，部分对应值如下表，y=f（x）的导函数y=f′（x）的图象如图所示．下列关于y=f（x）的命题：