题目内容
已知球的直径SC=6,A,B是该球球面上的两点,AB=3,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为 .
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:由题意求出SA=AC=SB=BC=3
,∠SAC=∠SBC=90°,说明过O,A,B的平面与SC垂直,求出三角形OAB的面积,即可求出棱锥S-ABC的体积.
| 2 |
解答:
 解:如图,由题意△ASC,△BSC均为等腰直角三角形,求出SA=AC=SB=BC=3
解:如图,由题意△ASC,△BSC均为等腰直角三角形,求出SA=AC=SB=BC=3
,
所以∠SOA=∠SOB=90°,所以SC⊥平面ABO.
又AB=3,△ABO为正三角形,则S△ABO=
×32=
,
进而可得:V S-ABC=V C-AOB+V S-AOB=
×
×6=
.
故答案为:
.
 解:如图,由题意△ASC,△BSC均为等腰直角三角形,求出SA=AC=SB=BC=3
解:如图,由题意△ASC,△BSC均为等腰直角三角形,求出SA=AC=SB=BC=3| 2 |
所以∠SOA=∠SOB=90°,所以SC⊥平面ABO.
又AB=3,△ABO为正三角形,则S△ABO=
| ||
| 4 |
9
| ||
| 4 |
进而可得:V S-ABC=V C-AOB+V S-AOB=
| 1 |
| 3 |
9
| ||
| 4 |
9
| ||
| 2 |
故答案为:
9
| ||
| 2 |
点评:本题是基础题,考查球的内接三棱锥的体积,考查空间想象能力,计算能力,得出SC⊥平面ABO是本题的解题关键,且用了体积分割法.

练习册系列答案
相关题目
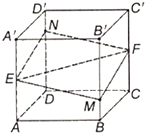 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M,N,设BM=x,x∈[0,1],给出以下五个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M,N,设BM=x,x∈[0,1],给出以下五个命题: 已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.若该四棱锥的侧视图为直角三角形,则它的体积为
已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.若该四棱锥的侧视图为直角三角形,则它的体积为