题目内容
14．已知集合A={x|0＜x＜5，x∈Z}，B={y|y=3n-2，n∈A}，则A∩B=（ ）| A． | {1} | B． | {4} | C． | {1，3} | D． | {1，4} |
分析 化简集合A、B，找出A与B的交集即可．
解答 解：集合A={x|0＜x＜5，x∈Z}={1，2，3，4}，
B={y|y=3n-2，n∈A}={1，4，7，10}，
则A∩B={1，4}，
故选：D
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．如图，网格纸上小正方形的边长为1，粗线画出的是一个四棱锥的三视图，则该四棱锥最长棱的棱长为（ ）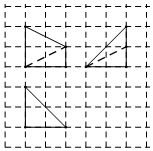
| A． | 3 | B． | $\sqrt{5}$ | C． | $2\sqrt{2}$ | D． | $2\sqrt{3}$ |
5．若复数z满足（$\sqrt{3}$-2i）z=6i（i是虚数单位），则z=（ ）
| A． | $\frac{-12+6\sqrt{3}i}{7}$ | B． | $\frac{3}{2}$-$\frac{\sqrt{3}}{2}$i | C． | $\frac{3}{2}$+$\frac{\sqrt{3}}{2}$i | D． | -$\frac{3}{2}$-$\frac{\sqrt{3}}{2}$i |
6．已知$a=\sqrt{3}$，$b={125^{\frac{1}{6}}}$，$c={log_{\frac{1}{6}}}\frac{1}{7}$，则下列不等关系正确的是（ ）
| A． | b＜a＜c | B． | a＜b＜c | C． | b＜c＜a | D． | c＜a＜b |
3．在△ABC中，角A，B，C的对边分别为a，b，c，已知△ABC的外接圆半径为R=$\sqrt{2}$，且tanB+tanC=$\frac{\sqrt{2}sinA}{cosC}$，则角B和边b的值分别为（ ）
| A． | $\frac{π}{6}$，$\sqrt{2}$ | B． | $\frac{π}{4}$，2 | C． | $\frac{π}{3}$，$\sqrt{6}$ | D． | $\frac{3π}{4}$，2 |
4．袋中有外观相同的红球，黑球各1个，现依次有放回地随机摸取3次，每次摸取1个球，若摸到红球时得2分，摸到黑球时得1分，则3次摸球所得总分为5的概率为（ ）
| A． | $\frac{5}{7}$ | B． | $\frac{6}{7}$ | C． | $\frac{3}{8}$ | D． | $\frac{5}{8}$ |