题目内容
19. 已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f'(x)的图象如图所示,且经过点(1,0),(2,0).
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f'(x)的图象如图所示,且经过点(1,0),(2,0).(1)求x0的值以及f(x)的解析式;
(2)若方程f(x)-m=0恰有2个根,求m的值.
分析 (1)结合图象求出函数的单调区间,从而求出x0的值以及f(x)的解析式;(2)结合(1)求出函数的极大值和极小值,求出m的值即可.
解答 解:(1)由题意得,
在(-∞,1)上,f′(x)>0,f(x)递增,
在(1,2)上,f′(x)<0,f(x)递减,
在(2,+∞)上,f′(x)>0,f(x)递增,
故f(x)极大值=f(1)=af(x0)=5,故x0=1,
f′(x)=3ax2+2bx+c,
由f′(1)=0,f′(2)=0,f(1)=5,
得$\left\{\begin{array}{l}{3a+2b+c=0}\\{12a+4b+c=0}\\{a+b+c=5}\end{array}\right.$,
解得:a=2,b=-9,c=12,
故f(x)=2x3-9x2+12x;
(2)若方程f(x)-m=0恰有2个根,
即m=f(x)有2个交点,
由(1)得:f(x)=2x3-9x2+12x,
f(x)极大值=f(1)=5,f(x)极小值=f(2)=4,
故m=5或m=4.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及转化思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.按如图的规律所拼成的一图案共有1024个大小相同的小正三角形“△”或“?”,则该图案共有( )


| A. | 16层 | B. | 32层 | C. | 64层 | D. | 128层 |
4.如图,网格纸上小正方形的边长为1,粗线画出的是一个四棱锥的三视图,则该四棱锥最长棱的棱长为( )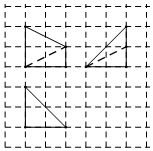

| A. | 3 | B. | $\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |