题目内容
12.当实数m为何值时,z=$\frac{{m}^{2}-m-6}{m+3}$+(m2+5m+6)i(1)为虚数;
(2)复数z对应的点在复平面内的第二象限内.
分析 (1)若z为虚数,则m2+5m+6≠0;
(2)若z对应的点在第二象限,则$\left\{\begin{array}{l}{\frac{{m}^{2}-m-6}{m+3}<0}\\{{m}^{2}+5m+6>0}\end{array}\right.$,解出即可得出.
解答 解:(1)若z为虚数,则m2+5m+6≠0,
∴m≠-2且m≠-3.
(2)若z对应的点在第二象限,则$\left\{\begin{array}{l}{\frac{{m}^{2}-m-6}{m+3}<0}\\{{m}^{2}+5m+6>0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m<-3或-2<m<3}\\{m<-3或m>-2}\end{array}\right.$.
∴m<-3或-2<m<3.
点评 本题考查了虚数的定义、几何意义、不等式的解法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
20.复数z=2-i在复平面对应的点在第几象限( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.按如图的规律所拼成的一图案共有1024个大小相同的小正三角形“△”或“?”,则该图案共有( )


| A. | 16层 | B. | 32层 | C. | 64层 | D. | 128层 |
4.如图,网格纸上小正方形的边长为1,粗线画出的是一个四棱锥的三视图,则该四棱锥最长棱的棱长为( )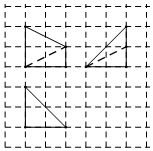

| A. | 3 | B. | $\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |