题目内容
9.求下列函数的导数(1)y=(2x2+3)(3x-1);
(2)y=xex+2x+1.
分析 根据导数的运算法则求导即可.
解答 解:(1)y=(2x2+3)(3x-1)=6x3-2x2+9x-3
∴y'=18x2-4x+9,
(2)y′=ex+xex+2.
点评 本题考查导数的运算法则,属于基础题.

练习册系列答案
相关题目
19.在△ABC中,角A,B,C的对边分别为a,b,c,且A=30°,B=15°,a=3,则c的值为( )
| A. | 6 | B. | $\frac{3}{2}$ | C. | 3$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
14.动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,其初始位置为A0($\frac{1}{2}$,$\frac{{\sqrt{3}}}{2}$),12秒旋转一周,则动点A的纵坐标y关于时间t(单位:秒)的函数解析式为( )
| A. | $y=sin(\frac{π}{3}t+\frac{π}{6})$ | B. | $y=cos(\frac{π}{6}t+\frac{π}{3})$ | C. | $y=sin(\frac{π}{6}t+\frac{π}{3})$ | D. | $y=cos(\frac{π}{3}t+\frac{π}{6})$ |
4.如图,网格纸上小正方形的边长为1,粗线画出的是一个四棱锥的三视图,则该四棱锥最长棱的棱长为( )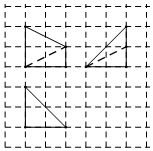

| A. | 3 | B. | $\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |