题目内容
若等差数列{an}中,a1=3,a4=12,{bn-an}为等比数列,且数列{bn}满足b1=4,b4=20.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用等差数列与等比数列的通项公式即可得出;
(2)利用等差数列与等比数列的前n项和公式即可得出.
(2)利用等差数列与等比数列的前n项和公式即可得出.
解答:
解:(1)设等差数列{an}的公差为d,∵a1=3,a4=12,∴12=3+3d,解得d=3.
∴an=a1+(n-1)d=3+3(n-1)=3n.
∵{bn-an}为等比数列,设公比为q,
又数列{bn}满足b1=4,b4=20.
∴b4-a4=(b1-a1)q3,即(20-12)=(4-3)q3,解得q=2.
∴bn-an=2n-1,
∴bn=3n+2n-1.
(2)由(1)可得数列{bn}的前n项和=3(1+2+…+n)+1+2+22+…+2n-1
=
+
=
+2n-1.
∴an=a1+(n-1)d=3+3(n-1)=3n.
∵{bn-an}为等比数列,设公比为q,
又数列{bn}满足b1=4,b4=20.
∴b4-a4=(b1-a1)q3,即(20-12)=(4-3)q3,解得q=2.
∴bn-an=2n-1,
∴bn=3n+2n-1.
(2)由(1)可得数列{bn}的前n项和=3(1+2+…+n)+1+2+22+…+2n-1
=
| 3n(n+1) |
| 2 |
| 2n-1 |
| 2-1 |
=
| 3n(n+1) |
| 2 |
点评:本题考查了等差数列与等比数列的通项公式、前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
正方体的外接球与其内切球的体积之比为 ( )
A、
| ||
| B、3:1 | ||
C、3
| ||
| D、9:1 |
将直线2x-y+λ=0沿x轴向右平移1个单位,所得直线与圆x2+y2+2x-4y=0相切,则实数λ的值为( )
| A、-3或7 | B、-2或8 |
| C、0或10 | D、1或11 |
从甲、乙、丙三人中任选2人作代表,则甲被选中的概率为( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
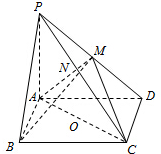 在四棱锥P-ABCD中,底面ABCD是矩形PA⊥ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.
在四棱锥P-ABCD中,底面ABCD是矩形PA⊥ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.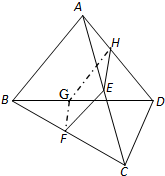 如图,在四面体ABCD中,平行于AB,CD的平面β截四面体所得截面为EFGH.
如图,在四面体ABCD中,平行于AB,CD的平面β截四面体所得截面为EFGH.