题目内容
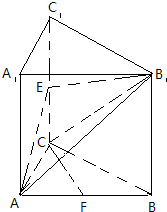 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB的中点,AC=BC=1,AA1=2.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB的中点,AC=BC=1,AA1=2.(1)求证:CF∥平面AB1E;
(2)求三棱锥C-AB1E的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)取AB中点M,连MF,ME,易证四边形MFCE是平行四边形,利用线面平行的判定定理即可证得CF∥平面AB1E;
(2)依题意,可证得BC⊥侧面AC1,利用等体积转换,即可求出三棱锥C-AB1E的体积.
(2)依题意,可证得BC⊥侧面AC1,利用等体积转换,即可求出三棱锥C-AB1E的体积.
解答:
 (1)证明:取AB中点M,连MF,ME,
(1)证明:取AB中点M,连MF,ME,
∵E为CC1中点,F为AB中点,
∴MF∥B1B,MF=
B1B,EC∥B1B,EC=
B1B,
∴MF∥EC,且MF=EC,
∴MFCE为平行四边形,
∴CF∥EM,
∵CF?平面AB1E,EM?平面AB1E,
∴CF∥平面AB1E.
(2)解:∵AA1⊥底面ABC,∴侧面AC1⊥底面ABC,
又∠ACB=90°,BC垂直于交线AC,∴BC⊥侧面AC1.
∵AC=BC=1,AA1=2,
∴S△ACE=
•1•1=
,
∴VO-AB1E=VB1-ACE=VB-ACE=
•
•1=
.
 (1)证明:取AB中点M,连MF,ME,
(1)证明:取AB中点M,连MF,ME,∵E为CC1中点,F为AB中点,
∴MF∥B1B,MF=
| 1 |
| 2 |
| 1 |
| 2 |
∴MF∥EC,且MF=EC,
∴MFCE为平行四边形,
∴CF∥EM,
∵CF?平面AB1E,EM?平面AB1E,
∴CF∥平面AB1E.
(2)解:∵AA1⊥底面ABC,∴侧面AC1⊥底面ABC,
又∠ACB=90°,BC垂直于交线AC,∴BC⊥侧面AC1.
∵AC=BC=1,AA1=2,
∴S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
∴VO-AB1E=VB1-ACE=VB-ACE=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题考查直线与平面平行的判定,考查线面垂直的性质,考查三棱锥的体积轮换公式的运用,考查推理证明与运算能力,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
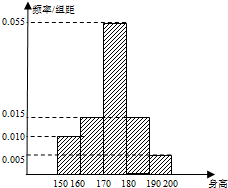 某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.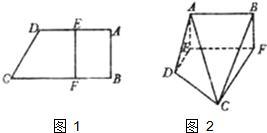 如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直.
如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直.