题目内容
函数f(x)=x2-x-2,x∈[-5,5],在定义域内任取一点x0,使f(x0)≥0的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:先解不等式f(x0)≥0,得能使事件f(x0)≥0发生的x0的取值长度为3,再由x0总的可能取值,长度为定义域长度10,得事件f(x0)≤0发生的概率是0.3
解答:
解:∵f(x)≥0?x2-x-2≥0?x≤-1或者x≥2,
∵在定义域内任取一点x0,
∴x0∈[-5,5],使f(x)≥0的区间为(-∞,-1]∪[2,+∞),
∴在定义域内,使f(x0)≥0的概率P=
=
=
故选D.
∵在定义域内任取一点x0,
∴x0∈[-5,5],使f(x)≥0的区间为(-∞,-1]∪[2,+∞),
∴在定义域内,使f(x0)≥0的概率P=
| -1-(-5)+5-2 |
| 5-(-5) |
| 4+3 |
| 10 |
| 7 |
| 10 |
故选D.
点评:本题考查了几何概型的意义和求法,将此类概率转化为长度、面积、体积等之比,是解决问题的关键

练习册系列答案
相关题目
阅读下列程序则该程序对应的程序框图(如图)中,①,②两个判断框内要填写的内容分别是( )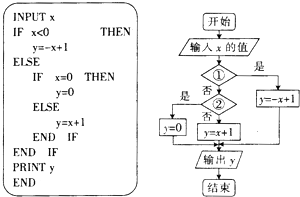

| A、x>0?x<0? |
| B、x>0?x=0 |
| C、x<0?x=0 |
| D、x≥0? x<0 |
要得到函数y=cos2x的图象,可由函数y=cos(2x-
)的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
五位同学参加某作家的签字售书活动,则甲、乙都排在丙前面的方法有( )
| A、20种 | B、24种 |
| C、40种 | D、56种 |
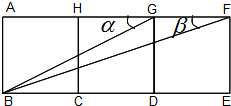 如图,有三个并排放在一起的正方形,∠AGB=α,∠AFB=β.
如图,有三个并排放在一起的正方形,∠AGB=α,∠AFB=β.