题目内容
“数列{an}(n∈N*)满足an+1=an•q(其中q为常数)”是“数列{an}(n∈N*)是等比数列”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:判断充要条件,先确定条件和结论,然后分成充分性和必要性判断.
解答:
解:条件p:“数列{an}(n∈N*)满足an+1=an•q(其中q为常数)”,结论q:“数列{an}(n∈N*)是等比数列”,
充分性:当数列为常数列an=0时,满足an+1=an•q(其中q为常数),但不是等比数列,充分性不满足,
必要性:数列{an}(n∈N*)是等比数列,根据等比数列定义,必有an+1=an•q,必要性成立,
所以“数列{an}(n∈N*)满足an+1=an•q(其中q为常数)”是“数列{an}(n∈N*)是等比数列”的必要不充分条件,
故选:B.
充分性:当数列为常数列an=0时,满足an+1=an•q(其中q为常数),但不是等比数列,充分性不满足,
必要性:数列{an}(n∈N*)是等比数列,根据等比数列定义,必有an+1=an•q,必要性成立,
所以“数列{an}(n∈N*)满足an+1=an•q(其中q为常数)”是“数列{an}(n∈N*)是等比数列”的必要不充分条件,
故选:B.
点评:本题考查充要条件的判断,关键是分清条件和结论.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
要得到函数y=cos2x的图象,可由函数y=cos(2x-
)的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知全集U={0,1,2,3,4,5},集合A={1,2,3,4},B={2,4},则(∁UA)∪B=( )
| A、{1,2,4} |
| B、{2,3,4} |
| C、{0,2,4,5} |
| D、{0,2,3,4} |
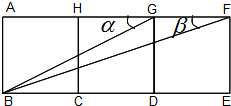 如图,有三个并排放在一起的正方形,∠AGB=α,∠AFB=β.
如图,有三个并排放在一起的正方形,∠AGB=α,∠AFB=β.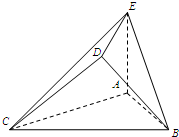 如图,△ABC是边长为2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
如图,△ABC是边长为2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.