题目内容
用一平面去截球所得截面的面积为2π，已知球心到该截面的距离为1，则该球的体积是（ ）
A、
| ||||
B、2
| ||||
C、4
| ||||
D、
|
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：求出小圆的半径，然后利用球心到该截面的距离为1，小圆的半径，通过勾股定理求出球的半径，即可求出球的体积．
解答：
解：用一平面去截球所得截面的面积为2π，所以小圆的半径为：
cm；
已知球心到该截面的距离为1，所以球的半径为：
，
所以球的体积为：
π×(
)3=4
π
故选：C．
| 2 |
已知球心到该截面的距离为1，所以球的半径为：
| 3 |
所以球的体积为：
| 4 |
| 3 |
| 3 |
| 3 |
故选：C．
点评：本题是基础题，考查球的小圆的半径，球心到该截面的距离，球的半径之间的关系，满足勾股定理，考查计算能力．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
如图所示，一个空间几何体的正视图和侧视图都是全等的等腰三角形，俯视图是一个圆，那么这个几何体是（ ）
| A、正方体 | B、圆锥 | C、圆柱 | D、半球 |
阅读下列程序则该程序对应的程序框图（如图）中，①，②两个判断框内要填写的内容分别是（ ）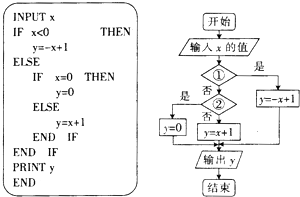
| A、x＞0？x＜0？ |
| B、x＞0？x=0 |
| C、x＜0？x=0 |
| D、x≥0？ x＜0 |
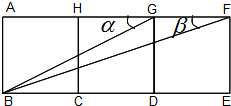如图，有三个并排放在一起的正方形，∠AGB=α，∠AFB=β．