题目内容
设复数z满足,且(
-3i)z=6i,则z= .
| 3 |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:把已知的等式变形,然后直接利用复数代数形式的乘除运算求解.
解答:
解:由(
-3i)z=6i,得
z=
=
=
=-
+
i.
故答案为:-
+
i.
| 3 |
z=
| 6i | ||
|
6i(
| ||||
(
|
-18+6
| ||
| 12 |
| 3 |
| 2 |
| ||
| 2 |
故答案为:-
| 3 |
| 2 |
| ||
| 2 |
点评:本题考查了复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
相关题目
已知全集U={0,1,2,3,4,5},集合A={1,2,3,4},B={2,4},则(∁UA)∪B=( )
| A、{1,2,4} |
| B、{2,3,4} |
| C、{0,2,4,5} |
| D、{0,2,3,4} |
已知等差数列{an}的前n项和为Sn,若S10<0,S11>0,则当Sn最小时n的值是( )
| A、7 | B、6 | C、5 | D、4 |
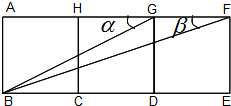 如图,有三个并排放在一起的正方形,∠AGB=α,∠AFB=β.
如图,有三个并排放在一起的正方形,∠AGB=α,∠AFB=β.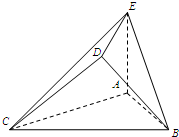 如图,△ABC是边长为2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
如图,△ABC是边长为2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.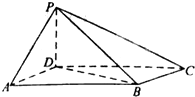 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,平面PAD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,平面PAD⊥底面ABCD.