题目内容
定义
*
=|a|×|b|sinθ,θ为
与
的夹角,已知点A(-3,2),点B(2,3),O是坐标原点,则
*
等于( )
| a |
| b |
| a |
| b |
| OA |
| OB |
| A、5 | B、13 | C、0 | D、-2 |
考点:平面向量数量积的运算,进行简单的合情推理
专题:新定义,平面向量及应用
分析:运用向量的坐标运算和向量的数量积的定义和坐标表示和向量的模,可得向量的夹角,再由新定义,计算即可得到所求值.
解答:
解:由点A(-3,2),点B(2,3),O是坐标原点,
则
=(-3,2),
=(2,3),
|
|=
=
,|
|=
=
,
由
•
=|
|•|
|cos<
,
>,
即有-3×2+2×3=
×
cos<
,
>,
即cos<
,
>=0,
由0≤<
,
>≤π,
则sin<
,
>=1,
即有
*
=|
|•|
|sin<
,
>
=
×
×1=13.
故选B.
则
| OA |
| OB |
|
| OA |
| 9+4 |
| 13 |
| OB |
| 4+9 |
| 13 |
由
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
即有-3×2+2×3=
| 13 |
| 13 |
| OA |
| OB |
即cos<
| OA |
| OB |
由0≤<
| OA |
| OB |
则sin<
| OA |
| OB |
即有
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
=
| 13 |
| 13 |
故选B.
点评:本题考查向量的数量积的定义和坐标表示,主要考查新定义
*
的理解和运用,运用同角的平方关系是解题的关键.
| a |
| b |

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
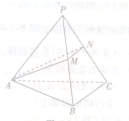 如图所示,在三棱锥P-ABC中,PA=PB=PC,底面△ABC是正三角形,M、N分别是侧棱PB、PC的中点,若平面AMN⊥平面PBC,则平面AMN与平面ABC成二面角(锐角)的余弦值等于( )
如图所示,在三棱锥P-ABC中,PA=PB=PC,底面△ABC是正三角形,M、N分别是侧棱PB、PC的中点,若平面AMN⊥平面PBC,则平面AMN与平面ABC成二面角(锐角)的余弦值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
中小学校车安全引起社会的关注,为了彻底消除校车安全隐患,某市购进了50台完全相同的校车,准备发放给10所学校,每所学校至少2台,则不同的发放方案种数为( )
A、
| ||
B、
| ||
C、
| ||
D、
|